Question

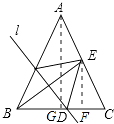
【题目】如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为 ．

Answer 1

【答案】13
【解析】解：过点A作AG⊥BC于点G，

∵AB=AC，BC=24，tanC=2，

∴ =2，GC=BG=12，

∴AG=24，

∵将△ABC沿直线l翻折后，点B落在边AC的中点处，

过E点作EF⊥BC于点F，

∴EF= AG=12，

∴ =2，

∴FC=6，

设BD=x，则DE=x，

∴DF=24﹣x﹣6=18﹣x，

∴x2=（18﹣x）2+122，

解得：x=13，

则BD=13．

所以答案是：13．

【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．