【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:
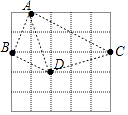
理由是:连接AC、AB、AD、BC、CD、BD,
设小正方形的边长为1,
由勾股定理得:AB2=12+22=5,AC2=22+42=20,AD2=12+32=10,BC2=52=25,CD2=12+32=10,BD2=12+22=5,
∴AB2+AC2=BC2,AD2+CD2=AC2,BD2+AB2=AD2,
∴△ABC、△ADC、△ABD是直角三角形,共3个直角三角形,
所以答案是:C.
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的长方体.

(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,当x>0时,y随x的增大而增大的是( )
A.y=﹣2x+1
B.y=﹣x2﹣1
C.y=(x+1)2﹣1
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角相等,即∠1=∠2.
如图②所示,AB,CD为两面平面镜,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你计算:图②中,当两平面镜AB,CD的夹角∠ABC是多少度时,可以使入射光线m与反射光线n平行但方向相反.

相关试题

