【题目】理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
=![]() =
=![]() .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=![]() .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =
=![]() .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)能相交,P(﹣1,﹣4)或(
;(3)能相交,P(﹣1,﹣4)或(![]() ,3).
,3).
【解析】
试题分析:(1)如图1,只需借鉴思路一或思路二的方法,就可解决问题;
(2)如图2,在Rt△ABC中,由勾股定理求出AB,由三角函数得出∠BAC=30°.从而得到∠DAB=75°.在Rt△ABD中,由三角函数就可求出DB,从而求出DC长;
(3)分类种情况讨论:①若直线AB绕点C逆时针旋转45°后,与双曲线相交于点P,如图3.过点C作CD∥x轴,过点P作PE⊥CD于E,过点A作AF⊥CD于F,可先求出点A、B、C的坐标,从而求出tan∠ACF的值,进而利用和(差)角正切公式求出tan∠PCE=tan(45°+∠ACF)的值,设点P的坐标为(a,b),根据点P在反比例函数的图象上及tan∠PCE的值,可得到关于a、b的两个方程,解这个方程组就可得到点P的坐标;②若直线AB绕点C顺时针旋转45°后,与x轴相交于点G,如图4,由①可知∠ACP=45°,P(![]() ,3),则有CP⊥CG.过点P作PH⊥y轴于H,易证△GOC∽△CHP,根据相似三角形的性质可求出GO,从而得到点G的坐标,然后用待定系数法求出直线CG的解析式,然后将直线CG与反比例函数的解析式组成方程组,消去y,得到关于x的方程,运用根的判别式判定,得到方程无实数根,此时点P不存在.
,3),则有CP⊥CG.过点P作PH⊥y轴于H,易证△GOC∽△CHP,根据相似三角形的性质可求出GO,从而得到点G的坐标,然后用待定系数法求出直线CG的解析式,然后将直线CG与反比例函数的解析式组成方程组,消去y,得到关于x的方程,运用根的判别式判定,得到方程无实数根,此时点P不存在.
试题解析:(1)方法一:如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tan∠DAC=tan75°=
.tan∠DAC=tan75°=![]() =
=![]() =
=![]() =
=![]() ;
;
方法二:tan75°=tan(45°+30°)=![]() =
=![]() =
=![]() =
=![]() ;
;
(2)如图2,在Rt△ABC中,AB=![]() =
=![]() =
=![]() ,sin∠BAC=
,sin∠BAC=![]() ,即∠BAC=30°.∵∠DAC=45°,∴∠DAB=45°+30°=75°.在Rt△ABD中,tan∠DAB=
,即∠BAC=30°.∵∠DAC=45°,∴∠DAB=45°+30°=75°.在Rt△ABD中,tan∠DAB=![]() ,∴DB=ABtan∠DAB=
,∴DB=ABtan∠DAB=![]() (
(![]() )=
)=![]() ,∴DC=DB﹣BC=
,∴DC=DB﹣BC=![]() =
=![]() .
.
答:这座电视塔CD的高度为(![]() )米;
)米;
(3)①若直线AB绕点C逆时针旋转45°后,与双曲线相交于点P,如图3.过点C作CD∥x轴,过点P作PE⊥CD于E,过点A作AF⊥CD于F.解方程组: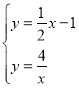 ,得:
,得:![]() 或
或![]() ,∴点A(4,1),点B(﹣2,﹣2).对于
,∴点A(4,1),点B(﹣2,﹣2).对于![]() ,当x=0时,y=﹣1,则C(0,﹣1),OC=1,∴CF=4,AF=1﹣(﹣1)=2,∴tan∠ACF=
,当x=0时,y=﹣1,则C(0,﹣1),OC=1,∴CF=4,AF=1﹣(﹣1)=2,∴tan∠ACF=![]() ,∴tan∠PCE=tan(∠ACP+∠ACF)=tan(45°+∠ACF)=
,∴tan∠PCE=tan(∠ACP+∠ACF)=tan(45°+∠ACF)=![]() =
=![]() =3,即
=3,即![]() =3.设点P的坐标为(a,b),则有:
=3.设点P的坐标为(a,b),则有: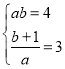 ,
,
解得:![]() 或
或![]() ,∴点P的坐标为(﹣1,﹣4)或(
,∴点P的坐标为(﹣1,﹣4)或(![]() ,3);
,3);
②若直线AB绕点C顺时针旋转45°后,与x轴相交于点G,如图4.由①可知∠ACP=45°,P(![]() ,3),则CP⊥CG.过点P作PH⊥y轴于H,则∠GOC=∠CHP=90°,∠GCO=90°﹣∠HCP=∠CPH,∴△GOC∽△CHP,∴
,3),则CP⊥CG.过点P作PH⊥y轴于H,则∠GOC=∠CHP=90°,∠GCO=90°﹣∠HCP=∠CPH,∴△GOC∽△CHP,∴![]() .∵CH=3﹣(﹣1)=4,PH=
.∵CH=3﹣(﹣1)=4,PH=![]() ,OC=1,∴
,OC=1,∴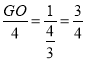 ,∴GO=3,G(﹣3,0).设直线CG的解析式为
,∴GO=3,G(﹣3,0).设直线CG的解析式为![]() ,则有:
,则有:![]() ,解得:
,解得: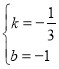 ,∴直线CG的解析式为
,∴直线CG的解析式为![]() .联立:
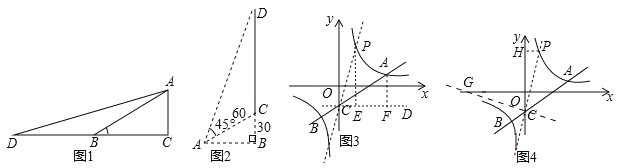
.联立: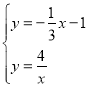 ,消去y,得:
,消去y,得:![]() ,整理得:
,整理得:![]() ,∵△=
,∵△=![]() ,∴方程没有实数根,∴点P不存在.
,∴方程没有实数根,∴点P不存在.
综上所述:直线AB绕点C旋转45°后,能与双曲线相交,交点P的坐标为(﹣1,﹣4)或(![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一组实数,
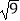 ,
, 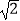 ,
,  , 1+
, 1+ 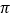 ,
, 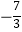 ,
, 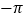
(1)将它们分类,填在相应的括号内:
有理数{ … };
无理数{ …};
(2)请你选出2个有理数和2个无理数, 再用 “+,-,×,÷” 中的3种不同的运算符号将选出的4个数进行运算(可以用括号), 使得运算的结果是一个正整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OB是∠AOC的平分线,OD是∠EOC的平分线.

(1)如果∠AOD=75°,∠BOC=19°,求∠DOE的度数。
(2)如果∠BOD=56°,求∠AOE的度数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍。乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠。该班需球拍5副,乒乓球若干盒(不小于5盒)。
问:
(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?
(3)当购买30盒乒乓球时,若让你选择一家商店去办这件事,你打算去哪家商店购买?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】化简(m2-n2)-(m+n)(m-n),得( )
A. -2m2 B. 0 C. 2m2 D. 2m2-2n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,∠A=80°,OB、OC分别平分∠ABC和∠ACB,你能求出∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.

(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
相关试题

