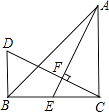
【题目】如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D. 
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
参考答案:
【答案】
(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵ 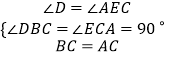
∴△DBC≌△ECA(AAS).
∴AE=CD
(2)解:由(1)得AE=CD,AC=BC,
在Rt△CDB和Rt△AEC中
![]() ,
,
∴Rt△CDB≌Rt△AEC(HL),
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC= ![]() BC=
BC= ![]() AC,且AC=12cm.
AC,且AC=12cm.
∴BD=6cm.
【解析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.(2)由(1)得BD=EC= ![]() BC=
BC= ![]() AC,且AC=12,即可求出BD的长.
AC,且AC=12,即可求出BD的长.
【考点精析】根据题目的已知条件,利用全等三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=
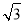 .tanD=tan15°=
.tanD=tan15°=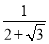 =
= =
= .
.思路二 利用科普书上的和(差)角正切公式:tan(α±β)=
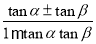 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=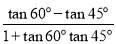 =
=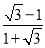 =
= .
.思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线
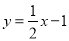 与双曲线
与双曲线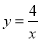 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(m2-n2)-(m+n)(m-n),得( )
A. -2m2 B. 0 C. 2m2 D. 2m2-2n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,∠A=80°,OB、OC分别平分∠ABC和∠ACB,你能求出∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识迁移
我们知道,函数
 的图像是由二次函数
的图像是由二次函数 的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数
的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数 的图像是由反比例函数
的图像是由反比例函数 的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).理解应用
函数
 的图像可以由函数
的图像可以由函数 的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .灵活运用
如图,在平面直角坐标系xOy中,请根据所给的
 的图像画出函数
的图像画出函数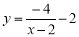 的图像,并根据该图像指出,当x在什么范围内变化时,
的图像,并根据该图像指出,当x在什么范围内变化时, ≥
≥ ?
?实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为
 ;若在
;若在 (
( ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为 .如果记忆存留量为
.如果记忆存留量为 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:3a﹣5a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值等于5的数是( )
A.5
B.-5
C.5或-5
D.不能确定
相关试题

