【题目】如图,观察每个正多边形中![]() 的变化情况,解答下列问题:
的变化情况,解答下列问题:
 ……
……
(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… |
|
| _________ | _________ | _________ | _________ | …… | _________ |
(2)根据规律,是否存在一个正![]() 边形,使其中的
边形,使其中的![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正![]() 边形,使其中的
边形,使其中的![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)60°,45°,36°,30°,![]() ;(2)当多边形是正九边形,能使其中的
;(2)当多边形是正九边形,能使其中的![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
(1)首先根据多边形的内角公式:(n-2)×180°,将n=3、4、5、6、8、12代入公式分别计算出各多边形的内角和;然后再根据多边形的外角和为360°,即可得到各多边形的内角和,进而完成表格.(2)依据题意得∠α=20°=![]() ,即可求出n的值。(3)依据题意∠α=21°=
,即可求出n的值。(3)依据题意∠α=21°=![]() ,求出n的值是否为正整数即可.
,求出n的值是否为正整数即可.
解:(1)填表如下:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | n |
|
|
|
|
| …… |
|
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(可以观察归纳出来,也可以计算出来).
;(可以观察归纳出来,也可以计算出来).
(2)存在一个正![]() 边形,使其中的
边形,使其中的![]()
理由是:根据题意得:![]() ,
,
解得:![]() ,
,
即当多边形是正九边形,能使其中的![]() ;
;
(3)不存在,理由如下:
假设存在正![]() 边形使得
边形使得![]() ,得
,得![]() ,
,
解得:![]() ,与
,与![]() 是正整数矛盾,
是正整数矛盾,
所以不存在正![]() 边形使得
边形使得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司决定更换节能环保的新型公交车
 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:A型数量
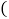 辆
辆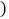
B型数量
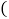 辆
辆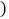
所需费用
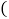 万元
万元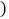
3
1
450
2
3
650
 求A型和B型公交车的单价;
求A型和B型公交车的单价; 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆? -
科目: 来源: 题型:
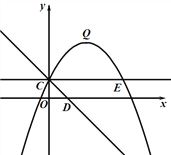
查看答案和解析>>【题目】如图,抛物线
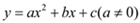 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
-
科目: 来源: 题型:
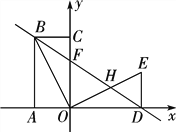
查看答案和解析>>【题目】如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1) 求直线BD的解析式;
(2) 求△BCF的面积;
(3) 点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
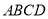 中,
中, 为
为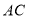 中点,过点
中点,过点 的直线分别与
的直线分别与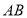 ,
,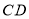 交于点
交于点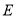 ,
,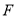 ,连结
,连结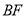 ,交
,交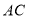 于点
于点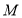 ,连结
,连结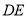 ,
,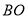 .若
.若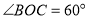 ,
,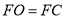 ,则下列结论:①
,则下列结论:① ;②
;②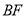 垂直平分线段
垂直平分线段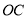 ;③
;③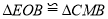 ;④四边形是
;④四边形是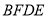 菱形.其中正确结论的个数是( )
菱形.其中正确结论的个数是( )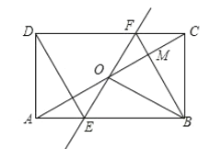
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B.  C.
C. 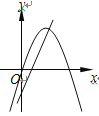 D.
D. 
相关试题

