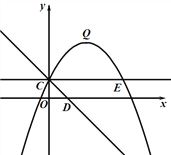
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)(2 , 3 )或
;(2)(2 , 3 )或![]() )或
)或![]() ;(3)存在,
;(3)存在, ![]() .
.
【解析】试题分析:
(1)根据已知条件设抛物线解析式为![]() ,代入点C的坐标就可以求出解析式了;
,代入点C的坐标就可以求出解析式了;
(2)①当点C是直角顶点时,由已知求出直线DM的解析式,再把所求解析式和(1)中所求二次函数解析式组合成方程组,解方程组即可求得点M的坐标;②当点D是直角顶点时,同①的方法可求得对应的M的坐标;
(3)如图3,分别作点C关于直线QE和直线OD的对称点C′和C′′,连接C′C′′交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度;如图4,连接C′E,作C′N⊥y轴于点N,结合已知条件解出C′C′′的长度即可.
试题解析:
(1)设抛物线的解析式为![]() ,
,
将C(0,1)代入得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为: ![]() 即
即![]() ;
;
(2)①如图1,当点C为直角顶点时,
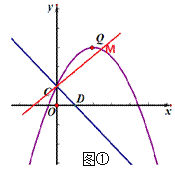
∵点C的坐标为(0,1),
∴OD=OC=1,
∴点D的坐标为(1,0),
设直线CD为![]() ,则:
,则: ![]() ,解答
,解答![]() ,
,
∴直线CD的解析式为: ![]() ,
,
∵此时CM⊥CD,
∴CM的解析式为: ![]() ,
,
由: 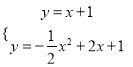 ,解得:
,解得: ![]() ,
, ![]() ,
,
∵点(0,1)与点C重合,
∴点M的坐标为(2,3),此时点M与点Q重合;
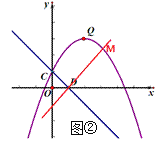
②如图②,当D为直角顶点时,由①可得直线DM的解析式为![]() ,
,
由:  ,解得:
,解得: 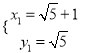 ,
, 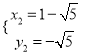 ,
,
∴点M的坐标为为![]() 或
或![]() ;
;
综上所述,符合题意的M有三点,分别是(2 , 3 ), ![]() 或
或![]() .
.
(3) 存在.如图③所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.
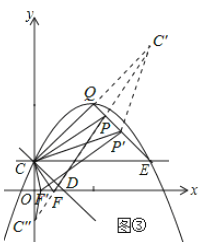
如答图④所示,连接C′E,
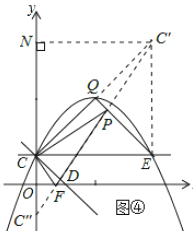
由(2)可知,QC⊥CD, 由题意可得:QC=QE,
∵∠DCE=45°,
∴∠QCE=45°=∠QEC,
∴△QCE是等腰直角三角形,
∵C,C′关于直线QE对称,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∵在抛物线![]() 中,由
中,由![]() 解得
解得![]() ,
,
∴点E的坐标为(4,1),
∴CE=4=C′E,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,
∴点C″的坐标为(0,﹣1).
∴OC″=1,
过点C′作C′N⊥y轴于点N,则NC′=CE=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″=![]() .
.
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个数的平方等于
 ,记为
,记为 ,这个数
,这个数 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为 (
( 为实数),
为实数), 叫这个复数的实部,
叫这个复数的实部,  叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:

(1)填空:
 =_________,
=_________,  =____________.
=____________.(2)填空:①
 _________; ②
_________; ② _________ .
_________ .(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知,
 ,(
,(  为实数),求
为实数),求 的值.
的值.(4)试一试:请利用以前学习的有关知识将
 化简成
化简成 的形式.
的形式.(5)解方程:x2 - 2x +4 = 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是一个4×4的正方形网格,每个小正方形的边长均为1.请在网格中以左上角的三角形为基本图形,通过平移、对称或旋转,设计两个精美图案,使其满足:①既是轴对称图形,又能以点
 为旋转中心旋转而得到;②所作图案用阴影标识,且阴影部分面积为4.
为旋转中心旋转而得到;②所作图案用阴影标识,且阴影部分面积为4.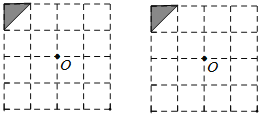
(2)如图,
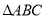 的三个顶点和点
的三个顶点和点 都在正方形网格的格点上,每个小正方形的边长都为1.
都在正方形网格的格点上,每个小正方形的边长都为1.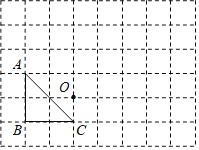
①将
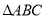 先向右平移4个单位,再向上平移2个单位得到
先向右平移4个单位,再向上平移2个单位得到 ,请画出
,请画出 ;
;②请画出
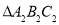 ,使
,使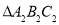 和
和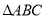 关于点
关于点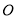 成中心对称;
成中心对称; -
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司决定更换节能环保的新型公交车
 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:A型数量
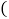 辆
辆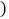
B型数量
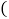 辆
辆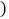
所需费用
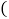 万元
万元
3
1
450
2
3
650
 求A型和B型公交车的单价;
求A型和B型公交车的单价; 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆? -
科目: 来源: 题型:
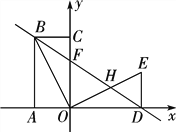
查看答案和解析>>【题目】如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1) 求直线BD的解析式;
(2) 求△BCF的面积;
(3) 点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,观察每个正多边形中
 的变化情况,解答下列问题:
的变化情况,解答下列问题: ……
……(1)将下面的表格补充完整:
正多边形的边数
3
4
5
6
……

 的度数
的度数_________
_________
_________
_________
……
_________
(2)根据规律,是否存在一个正
 边形,使其中的
边形,使其中的 ?若存在,写出
?若存在,写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)根据规律,是否存在一个正
 边形,使其中的
边形,使其中的 ?若存在,写出
?若存在,写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
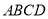 中,
中, 为
为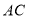 中点,过点
中点,过点 的直线分别与
的直线分别与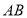 ,
,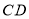 交于点
交于点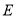 ,
,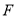 ,连结
,连结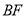 ,交
,交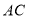 于点
于点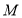 ,连结
,连结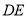 ,
,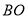 .若
.若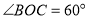 ,
,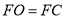 ,则下列结论:①
,则下列结论:① ;②
;②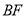 垂直平分线段
垂直平分线段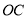 ;③
;③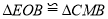 ;④四边形是
;④四边形是 菱形.其中正确结论的个数是( )
菱形.其中正确结论的个数是( )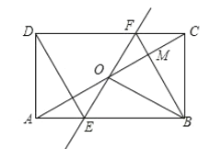
A.1个B.2个C.3个D.4个
相关试题

