搜索
【题目】在平面直角坐标系中，已知反比例函数y＝
的图象经过点A(1，
)．
(1)试确定此反比例函数的解析式；
(2)点O是坐标原点，将线OA绕O点顺时针旋转30°得到线段OB，判断点B是否在此反比例函数的图象上，并说明理由．
参考答案：
【答案】（1）y＝
；（2）在，理由见解析
【解析】
（1）把点A坐标代入反比例函数解析式，求出k值即可；（2）过点A作x轴的垂线交x轴于点C.过点B作x轴的垂线交x轴于点D.利用勾股定理可求出OA的长，进而可得∠OAC=30°，∠AOC＝60°，由旋转的性质可得∠AOB=30°，即可求出∠BOD的度数，进而可得BD、OD的长，即可得B点坐标，把B点横坐标代入解析式即可得答案.
(1)把A(1，
)代入y＝
，得k＝1×＝，
∴反比例函数的解析式为y＝
.
(2)过点A作x轴的垂线交x轴于点C.
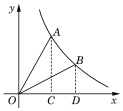
在Rt△AOC中，OC＝1，AC＝.
由勾股定理，得OA＝
＝2，
∴∠OAC=30°，∠AOC＝60°.
过点B作x轴的垂线交x轴于点D.
由题意，∠AOB＝30°，OB＝OA＝2，
∴∠BOD＝30°，
在Rt△BOD中，得BD＝1，OD＝，
∴B点坐标为(，1)．
将x＝代入y＝中，得y＝1，
∴点B(，1)在反比例函数y＝的图象上.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形OABC的顶点A的坐标为（0，1），点B的坐标为（1，2），∠ABC＝90°，连接AC．
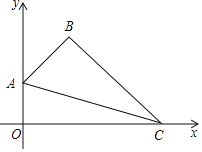
（1）求直线AC的函数表达式；
（2）点P是线段OC上一动点，从点O向点C运动，过点P作PM∥y轴，分别交AB或BC，AC于点M，N，其中点P的横坐标为m，MN的长为n．
①当0＜m≤1时，求n与m之间的函数关系式；
②当△AMN的面积最大时，请直接写出m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）（探索发现）
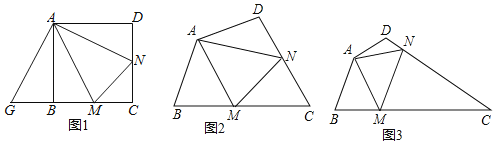
如图1，在正方形ABCD中，点M，N分别是边BC，CD上的点，∠MAN＝45°，若将△DAN绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为8，则正方形ABCD的边长为 ．
（2）（类比延伸）
如图2，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M，N分别在边BC，CD上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．
（3）（拓展应用）
如图3，在四边形ABCD中，AB＝AD＝2，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，AN，△ABM是等边三角形，AM⊥AD于点A，∠DAN＝15°，请直接写出△CMN的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y＝﹣
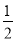x2+bx+c与x轴交于点A，B，其中点B的坐标为（4，0），与y轴交于点C（0，2）．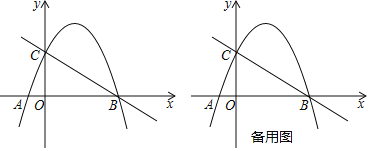
（1）求抛物线y＝﹣
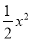+bx+c和直线BC的函数表达式；（2）点P是直线BC上方的抛物线上一个动点，当点P到直线BC的距离最大时，求点P的坐标；
（3）连接点O与（2）中求出的点P，交直线BC于点D，点N是直线BC上的一个动点，连接ON，作DF⊥ON于点F，点F在线段ON上，当OD＝
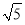DF时，请直接写出点N的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，反比例函数y＝
的图象与一次函数y＝k(x－2)的图象交点为A(3，2)，B(x，y)．(1)求反比例函数与一次函数的解析式及B点坐标；
(2)若C是y轴上的点，且满足△ABC的面积为10，求C点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化，开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？
（2）一道数学竞赛题，需要讲16分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？
-
科目： 来源： 题型：
查看答案和解析>>【题目】使用家用燃气灶烧开同一壶水所需的燃气量
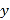（单位：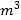
）与旋钮的旋转角度
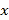（单位：度）（
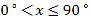）近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度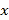与燃气量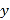的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A.
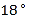B. 
C. 
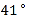D.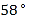 
相关试题
