搜索
【题目】使用家用燃气灶烧开同一壶水所需的燃气量
（单位：
）与旋钮的旋转角度
（单位：度）（
）近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度与燃气量的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】C
【解析】
根据已知三点和近似满足函数关系y=ax2+bx+c(a≠0)可以大致画出函数图像，并判断对称轴位置在36和54之间即可选择答案.
解：由图表数据描点连线，补全图像可得如图，
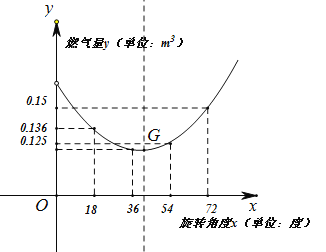
抛物线对称轴在36和54之间，约为41℃
∴旋钮的旋转角度
在36°和54°之间，约为41℃时，燃气灶烧开一壶水最节省燃气.
故选：C，
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知反比例函数y＝
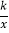的图象经过点A(1，
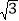)．(1)试确定此反比例函数的解析式；
(2)点O是坐标原点，将线OA绕O点顺时针旋转30°得到线段OB，判断点B是否在此反比例函数的图象上，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，反比例函数y＝
的图象与一次函数y＝k(x－2)的图象交点为A(3，2)，B(x，y)．(1)求反比例函数与一次函数的解析式及B点坐标；
(2)若C是y轴上的点，且满足△ABC的面积为10，求C点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化，开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？
（2）一道数学竞赛题，需要讲16分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
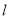已知：直线
及直线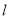外一点P.
求作：直线
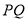，使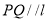
.作法：如图，
①在直线
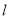上取一点O，以点O为圆心，
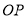长为半径画半圆，交直线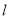于
两点；②连接
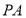，以B为圆心，
长为半径画弧，交半圆于点Q；③作直线
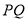.所以直线
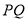就是所求作的直线.根据小明设计的尺规作图过程：
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明
证明：连接
，∵
，∴
__________.∴
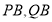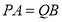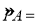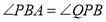（______________）（填推理的依据）.∴
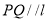（_____________）（填推理的依据）. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形；
（2）若AB＝
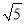，BD＝2，求OE的长．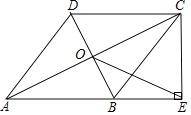
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况，从甲、乙两校各随机抽取40名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．
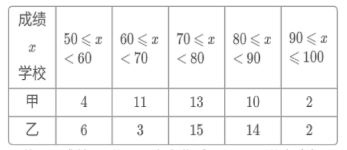
a．甲、乙两校40名学生成绩的频数分布统计表如下：
成绩x
学校
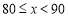
甲
4
11
13
10
2
乙
6
3
15
14
2
（说明：成绩80分及以上为优秀，70~79分为良好，60~69分为合格，60分以下为不合格）
b．甲校成绩在
这一组的是：70 70 70 71 72 73 73 73 74 75 76 77 78
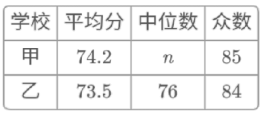
c．甲、乙两校成绩的平均分、中位数、众数如下：
学校
平均分
中位数
众数
甲
74.2
n
5
乙
73.5
76
84
根据以上信息，回答下列问题：
（1）写出表中n的值；
（2）在此次测试中，某学生的成绩是74分，在他所属学校排在前20名，由表中数据可知该学生是_____________校的学生（填“甲”或“乙”），理由是__________；
（3）假设乙校800名学生都参加此次测试，估计成绩优秀的学生人数．
相关试题
