【题目】△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向
以1cm/s的速度向点B运动(运动前点M与点A重合).过M,N分别作AB的垂线交直角边于P,Q两点,线段MN运动的时间为ts.
(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
(3)t为何值时,以C,P,Q为顶点的三角形与△ABC相似?

参考答案:
【答案】(1)y与t的函数关系式为
(2)当![]() 时,四边形MNQP为矩形 ;
时,四边形MNQP为矩形 ;
(3)当![]() 或
或![]() 时,以C,P,Q为顶点的三角形与△ABC相似.
时,以C,P,Q为顶点的三角形与△ABC相似.
【解析】试题分析:(1)分两种情况,点P可以在AC上时和当点P在BC上时,利用三角函数分别用含t的代数式表示出PM,AM,再用S△APM=![]() AMPM得出y与t的函数关系式,(2)当PM=QN时,四边形MNQP为矩形,建立含t的方程,求得t的值,(3)以C,P,Q为顶点的三角形与△ABC相似有两种情况,△PQC∽△ABC时和△QPC∽△ABC,分别相似三角形的判定和性质,求得相对应的t的值.
AMPM得出y与t的函数关系式,(2)当PM=QN时,四边形MNQP为矩形,建立含t的方程,求得t的值,(3)以C,P,Q为顶点的三角形与△ABC相似有两种情况,△PQC∽△ABC时和△QPC∽△ABC,分别相似三角形的判定和性质,求得相对应的t的值.
试题解析:(1)当点P在AC上时,
∵AM=t ,
![]()
![]()
当点P在BC上时,
![]()
![]()
(2)∵AC=2,∴AB=4,∴BN=AB-AM-MN=4-t=3-t
![]()
由条件可知,若四边形MNQP为矩形,需PM=QN,
![]()
![]()
![]() ,
,
![]()
∴△PQC∽△ABC,
除此之外,当∠CPQ=∠B=30°时,△QPC∽△△ABC,
![]() ,
,
![]()
∴AP=2AM=2t,
∴CP=2-2t,
![]() ,
,
 ,
,
![]()
![]()

![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何( )
A. 36
B. 72
C. 108
D. 144
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣x﹣20=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件 , 使四边形BECF是正方形.
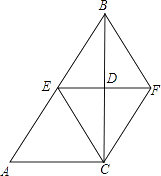
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=
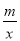 的图象的两个交点.
的图象的两个交点.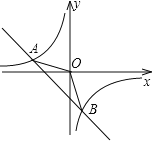
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣
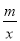 <0的解集.
<0的解集.(3)P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标。
相关试题

