【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
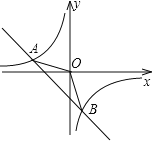
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣![]() <0的解集.
<0的解集.
(3)P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标。
参考答案:
【答案】(1)反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣x﹣2;
,一次函数的解析式为y=﹣x﹣2;
(2)不等式解集为﹣4<x<0或x>2;
(3)点P坐标为(-5,0),或(1,0)
【解析】试题分析:对于(1),由A(-4,n),B(2,4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点,利用待定系数法分别求出一次函数y=kx+b和反比例函数y= y=
的图象的两个交点,利用待定系数法分别求出一次函数y=kx+b和反比例函数y= y=![]() ;
;
对于(2),根据图象的增减性可直接得到答案.
对于(3)由S△APB=S△ACP+S△BPC可得PC=3,点C的坐标为(﹣2,0),点P 分在C点左侧和右侧两种情况求坐标.
试题解析:(1)∵B(2,﹣4)在y= y=![]() 上,
上,
∴m=﹣8.
∴反比例函数的解析式为y=﹣![]() .
.
∵点A(﹣4,n)在y=﹣![]() 上,
上,
∴n=2.
∴A(﹣4,2).
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴![]() ,解得:
,解得: ![]() .
.
∴一次函数的解析式为y=﹣x﹣2.
(2)不等式kx+b﹣y=![]() <0的解集为﹣4<x<0或x>2.
<0的解集为﹣4<x<0或x>2.
(3)∵S△APB=S△ACP+S△BPC
∴![]()
∴PC=3
∵y=0时,x=﹣2.∴点C(﹣2,0).
当P在C点的左侧时,P1(-5,0),当P在C点的右侧时,P2(1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向
以1cm/s的速度向点B运动(运动前点M与点A重合).过M,N分别作AB的垂线交直角边于P,Q两点,线段MN运动的时间为ts.
(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
(3)t为何值时,以C,P,Q为顶点的三角形与△ABC相似?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣x﹣20=0.
-
科目: 来源: 题型:
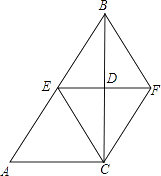
查看答案和解析>>【题目】如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件 , 使四边形BECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的10
 5(行
5(行 列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为
列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为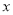 .
.(1)用含
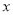 的式子表示另外三个数;
的式子表示另外三个数;(2)若这样框中的四个数的和是200,求出这四个数;
(3)是否存在这样的四个数,它们的和为246?为什么?
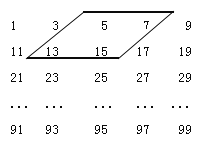
【答案】(1)x+2,x+8,x+10;(2)45,47,53,55;(3)不存在.
【解析】试题分析:(1)观察图框中的四个数,根据这四个数之间的数量关系,直接写出答案即可;(2)根据框中的四个数的和是200,列出方程,解方程即可;(3)根据框中的四个数的和是246,列出方程,解方程,根据方程解得情况判断是否存在即可.
试题解析:
(1)
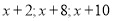 .
.(2)根据题意得:
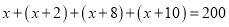 ,
,解之得,
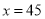 .
.∴x+2=47,x+8=53,x+10=55.
答:这四个数分别为45、47、53、55.
(3)不存在.
由
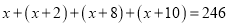 .
.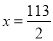 .
.而奇数是整数,所以不存在满足条件的数.
【题型】解答题
【结束】
25【题目】某单位计划购买电脑若干台,经了解同一型号市场预售价均为每台5000元.现有两商场优惠促销,甲商场:购买不超过2台按原价销售,超过2台的部分每台打7折;乙商场:每台均打8折.
(1)若学校购买5台,哪家商场较优惠?购买7台呢?
(2)买多少台时两商场所需费用一样多?
(3)你知道学校怎样选购更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C,D,E三点在直线AB上,P为直线AB外一点,PC=1,PD=2,PE=3,则点P到直线AB的距离( )
A. 小于1B. 不小于1C. 大于1D. 不大于1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 . 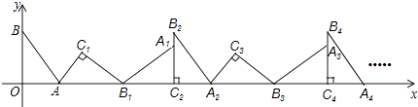
相关试题

