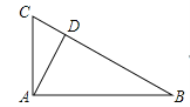
【题目】如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
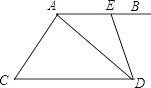
(1)求证:AD平分∠CDE;
(2)若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.
参考答案:
【答案】(1)见解析;(2)55°
【解析】
(1)根据平行线的性质得到∠BED=∠EDC,∠BAD=∠ADC,利用等量代换得到∠EDC=2∠ADC,由角平分线的定义即可得到结论;
(2)利用列方程的方式,设∠ADC=∠ADE=∠BAD=x,于是得到∠BED=∠EDC=2x,∠AED=180°-2x,根据平行线的性质得到∠BAC+∠ACD=180°,于是列方程90°-x+180°-2X=165°,即可得到结论.
(1)证明:∵AB∥CD,
∴∠BED=∠EDC,∠BAD=∠ADC,
∵∠BED=∠BAD+∠ADE,
∵∠BED=2∠BAD,
∴∠BAD=∠ADE,∠ADE=∠ACD,
∴AD平分∠CDE;
(2)解:依题意设∠ADC=∠ADE=∠BAD=x,
∴∠BED=∠EDC=2x,∠AED=180°﹣2x,
∵AB∥CD,
∴∠BAC+∠ACD=180°,即∠ACD=90°﹣x,
又∵∠ACD+∠AED=165°,
即90°﹣x+180°﹣2x=165°,
∴x=35°,
∴∠ACD=90°﹣x=90°﹣35°=55°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系并证明. (提示:延长CD到G,使得DG=BE)
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西20°的A处,舰艇乙在指挥中心南偏东60°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.(可利用(2)的结论)
-
科目: 来源: 题型:
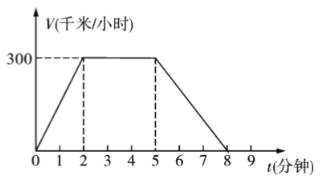
查看答案和解析>>【题目】如图,是一辆列车在某次运行中速度
 (千米/小时)关于时间
(千米/小时)关于时间 (分钟)的图象,根据图象回答下列问题.
(分钟)的图象,根据图象回答下列问题.(1)列车共运行了多少分钟?
(2)列车开动后,匀速行驶了几分钟?第3分钟时的速度是多少?
(3)列车的速度从0千米/小时加速到300千米/小时,共用了多长时间?
(4)列车从第几分钟开始减速?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩“石头、剪子、布”游戏,他们在不透明的袋子中放人形状、大小均相同的18张卡片,其中写有“石头”、“剪子”、“布”的卡片张数分别为5、6、7.两人先后各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“剪子”的概率是多少?
(2)若甲先摸出了“剪子”,则乙获胜的概率是多少?
(3)若甲先摸出了“布”,则甲获胜的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ΔABC中,AB=AC,∠A=36°,BE平分∠ABC,DE//BC,则图中等腰三角形共有( )个
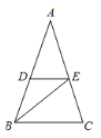
A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2017,则m的值是( )
A. 43 B. 44 C. 45 D. 46
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,AD是斜边BC上的高,∠B=30°,那么线段BD与CD的数量关系为( )
A. BD=CDB. BD=2CDC. BD=3CDD. BD=4CD
相关试题

