【题目】解答题唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
注:古代一斗是10升.
大意是:李白在郊外春游时,做出这样一条约定:遇 见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.
(1)列方程求壶中原有多少升酒;
(2)设壶中原有a0升酒,在第n个店饮酒后壶中余an升酒,如第一次饮后所余酒为a1=2a0﹣19(升),第二次饮后所余酒为a2=2a1﹣19=2(2a0﹣19)﹣19=22a0﹣(21+1)×19(升),….
①用an﹣1的表达式表示an , 再用a0和n的表达式表示an;
②按照这个约定,如果在第4个店喝光了壶中酒,请借助①中的结论求壶中原有多少升酒.
参考答案:
【答案】解:(1)设壶中原有x升酒.
依题意得:2[2(2x﹣19)﹣19]﹣19=0,
去中括号,得4(2x﹣19)﹣3×19=0.
去括号,得:8x﹣7×19=0.
系数化1,得x=16![]() ,
,
答:壶中原有16![]() 升酒;
升酒;
(2)①an=2an﹣1﹣19,
an=2na0﹣(2n﹣1+2n﹣2+…+1)×19,
(或an=2na0﹣(2n﹣1)×19);
②当n=4时,a4=24a0﹣(23+22+21+1)×19.
(或写成a4=24a0﹣(24﹣1)×19)
∵在第4个店喝光了壶中酒,
∴24a0﹣(23+22+21+1)×19=0,
(或写成24a0﹣(24﹣1)×19=0)
即16a0﹣15×19=0.
解得:a0=17![]() ,
,
答:在第4个店喝光了壶中酒时,壶中原有17![]() 升酒.
升酒.
【解析】(1)分别表示出酒壶中剩余的酒量,利用在第3个店里遇到朋友正好喝光了壶中的酒进而得出等式求出答案;
(2)①利用已知第一次饮后所余酒为a1=2a0﹣19(升),第二次饮后所余酒为a2=2a1﹣19=2(2a0﹣19)﹣19=22a0﹣(21+1)×19(升),…,进而用a0和n的表达式表示an;
②利用①中所求,进而代入求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1与∠2互余,∠2与∠3互补,∠1=58°,则∠3=( )
A. 58° B. 148° C. 158° D. 32°
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,青年旅行社组织一个团;老师和学生共50人组成的旅行团到凤凰古城旅游,景区门票售票标准是:成人门票50元/张,学生门票20元/张,该旅行团购买门票共花费1800元,若设该团购买成人门票x张,则可列方程为:____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理判断题七年级五个班的班长因为参加校学生干部培训会而没有观看年级的乒乓球比赛.年级组长让他们每人猜一猜其中两个班的比赛名次.这五个班长各自猜测的结果如表所示:
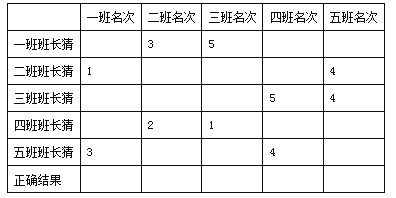
年级组长说,每班的名次都至少被他们中的一人说对了,请你根据以上信息将一班~五班的正确名次填写在表中最后一行. -
科目: 来源: 题型:
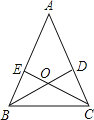
查看答案和解析>>【题目】如图,△ABC中,AB=AC,两条角平分线BD、CE相交于点O.
(1)证明:△ABD≌△ACE;(2)证明:OB=OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
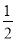 x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的解析式;
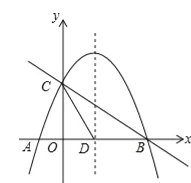
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知右表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.

相关试题

