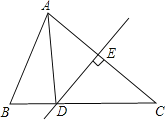
【题目】已知:在△ABC中,DE是AC的垂直平分线,AE=3.
①若AC=BC,求BC;
②若△ABD的周长为13,求△ABC的周长.
参考答案:
【答案】(1)6;(2)19.
【解析】
(1)根据线段的垂直平分线性质求出AC即可;
(2)根据线段的垂直平分线性质求出AD=DC,AC=2AE=6,根据△ABD的周长为13求出AB+BC的值即可求出答案.
(1)∵DE是AC的垂直平分线,AE=3,
∴AC=2AE=6,
∴AC=BC=6,
答:BC的长是6.
(2)∵DE是AC的垂直平分线,AE=3,
∴AD=DC,AC=2AE=6,
∵△ABD的周长为13,
∴AB+AD+BD=13,
∴AB+CD+BD=13,
即AB+BC=13,
∴△ABC的周长是AB+BC+AC=13+6=19.
答:△ABC的周长是19.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为
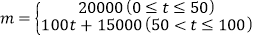 ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

-
科目: 来源: 题型:
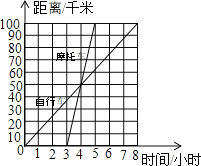
查看答案和解析>>【题目】如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象回答或解决下面的问题.
(1)谁出发的较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)指出在什么时间段内两车均行驶在途中;在这段时间内,
①自行车行驶在摩托车前面;
②自行车与摩托车相遇;
③自行车行驶在摩托车后面?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用100厘米长的铅丝,弯折成一个长方形的模型.
(1)设长方形的面积为S平方厘米,长方形的长为
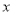 厘米,用
厘米,用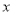 的式子表示S;
的式子表示S;(2)当S=400平方厘米时,求
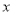 的值;
的值;(3)当S=625平方厘米时,求
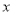 的值;
的值;(4)S的值会不会为700平方厘米?
-
科目: 来源: 题型:
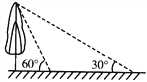
查看答案和解析>>【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表中给出的是某月的月历,任意选取“
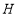 ”型框中的
”型框中的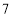 个数(如阴影部分所示).请你运用所学的数学知识来研究,则这
个数(如阴影部分所示).请你运用所学的数学知识来研究,则这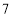 个数的和不可能是( )
个数的和不可能是( )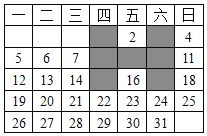
A.
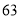 B.
B.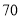 C.
C.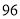 D.
D.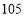
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高科技创新意识,我市某中学在“2018年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),根据各类别参赛人数制成不完全的条形统计图和扇形统计图如下:
请根据以上图品信息,解答下列问题:


(1)全体参赛的学生共有_______人,扇形统计图中“建模”所在扇形的圆心角是_______°;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生.现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动.则选取的两人中恰为1名男生1名女生的概率是______.
相关试题

