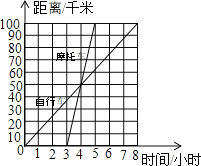
【题目】如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象回答或解决下面的问题.
(1)谁出发的较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)指出在什么时间段内两车均行驶在途中;在这段时间内,
①自行车行驶在摩托车前面;
②自行车与摩托车相遇;
③自行车行驶在摩托车后面?
参考答案:
【答案】(1)自行车,3,摩托车,3;(2)自行车:12.5千米/时;摩托车:50千米/时;(3)3<t<5;①3<t<4;②t=4;③4<t<5.
【解析】
(1)观察图即可解答;
(2)根据图中信息找出路程,时间,再求出速度;
(3)根据图象进行分析即可解答.
(1)由图可以看出,自行车出发较早,早3个小时,摩托车到达乙地较早,早3个小时;
(2)对自行车而言,行驶的距离是100千米,耗时8个小时.
所以其速度是:100÷8=12.5(千米/时);
对摩托车而言,行驶的距离是100千米,耗时2个小时.
所以其速度是:100÷2=50(千米/时);
(3)在3<t<5时间段内两车均行驶在途中.
当3<t<4时,自行车在摩托车前面;
当t=4时,两车相遇;
当4<t<5时,自行车在摩托车的后面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=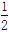 ,OB=4,OE=2.
,OB=4,OE=2.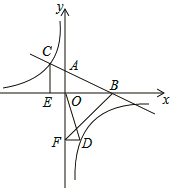
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=
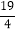 ,tan∠BAD=
,tan∠BAD=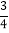 ,求⊙O的半径.
,求⊙O的半径.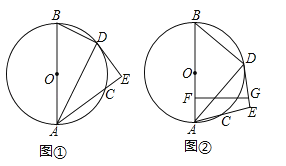
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为
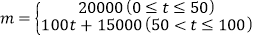 ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

-
科目: 来源: 题型:
查看答案和解析>>【题目】用100厘米长的铅丝,弯折成一个长方形的模型.
(1)设长方形的面积为S平方厘米,长方形的长为
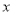 厘米,用
厘米,用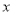 的式子表示S;
的式子表示S;(2)当S=400平方厘米时,求
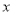 的值;
的值;(3)当S=625平方厘米时,求
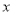 的值;
的值;(4)S的值会不会为700平方厘米?
-
科目: 来源: 题型:
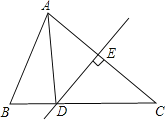
查看答案和解析>>【题目】已知:在△ABC中,DE是AC的垂直平分线,AE=3.
①若AC=BC,求BC;
②若△ABD的周长为13,求△ABC的周长.
-
科目: 来源: 题型:
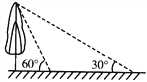
查看答案和解析>>【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
相关试题

