【题目】如图,点![]() 为定点,定直线
为定点,定直线![]() ,
,![]() 是直线上一动点,点
是直线上一动点,点![]() 分别为
分别为![]() 的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点
的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点![]() 的移动而变化的是( )
的移动而变化的是( )

A.②③B.②⑤C.①③④D.④⑤
参考答案:
【答案】C
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=![]() AB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
AB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MN=![]() AB,
AB,
即线段MN的长度不变,故①正确;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②错误;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③正确;
直线MN,AB之间的距离不随点P的移动而变化,故④正确;
∠APB的大小点P的移动而变化,故⑤错误。
综上所述,不会随点P的移动而变化的是①③④,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连接BD,过点E作EH⊥BD,垂足为H,连接EF,交BD于点G,交BC于点M,连接CF. 给出下列结论:①△CDE∽△CBF;②∠DBC=∠EFC;③
 ;④GH的值为定值
;④GH的值为定值 ;上述结论中正确的个数为( )
;上述结论中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个

①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A. (x2500)(8+4×
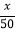 )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×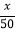 )=5000
)=5000C. (x2500)(8+4×
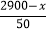 )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×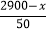 )=5000
)=5000 -
科目: 来源: 题型:
查看答案和解析>>【题目】同学报名次参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示)
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为___________;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1,利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=
 ∠CDN,∠CBE=
∠CDN,∠CBE= ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

相关试题

