【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

参考答案:
【答案】图见解析,小亮影子的长度为2m.
【解析】试题分析:(1)直接连接点光源和物体顶端形成的直线与地面的交点即是影子的顶端;
(2)根据中心投影的特点可知△CAB∽△CPO,利用相似比即可求解.
试题解析:
解:(1)连接PA并延长交地面于点C,线段BC就是小亮在照明灯(P)照射下的影子.

(2)在△CAB和△CPO中,
∵∠C=∠C,∠ABC=∠POC=90°
∴△CAB∽△CPO,
∴![]() ,
,
∴![]() ,
,
∴BC=2m,
∴小亮影子的长度为2m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 为定点,定直线
为定点,定直线 ,
, 是直线上一动点,点
是直线上一动点,点 分别为
分别为 的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点
的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点 的移动而变化的是( )
的移动而变化的是( )
A.②③B.②⑤C.①③④D.④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学报名次参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示)
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为___________;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1,利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=
 ∠CDN,∠CBE=
∠CDN,∠CBE= ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
-
科目: 来源: 题型:
查看答案和解析>>【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:|6+7|=6+7;|6﹣7|=7﹣6;|7﹣6|=7﹣6;|﹣6﹣7|=6+7
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7﹣21|= ;②|﹣
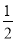 ﹣0.8|= ;③|
﹣0.8|= ;③|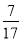 ﹣
﹣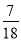 |= :
|= :(2)数a在数轴上的位置如图所示,则|a﹣2.5|= .

A.a﹣2.5
B.2.5﹣a
C.a+2.5
D.﹣a﹣2.5
(3)利用上述介绍的方法计算或化简:
①|
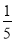 ﹣
﹣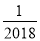 |+|
|+|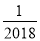 ﹣
﹣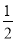 |﹣|﹣
|﹣|﹣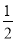 |+
|+ ;
;②|
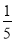 ﹣
﹣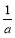 |+|
|+|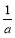 ﹣
﹣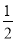 |﹣|﹣
|﹣|﹣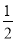 |+2(
|+2(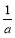 ),其中a>2.
),其中a>2.
相关试题

