【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
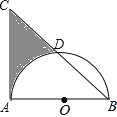
A. 16 B. 24-4π C. 32-4π D. 32-8π
参考答案:
【答案】B
【解析】试题分析:连接AD,因为△ABC是等腰直角三角形,故∠ABD=45°,再由AB是圆的直径得出∠ADB=90°,故△ABD也是等腰直角三角形,所以![]() ,S阴影=S△ABC-S△ABD-S弓形AD由此可得出结论.
,S阴影=S△ABC-S△ABD-S弓形AD由此可得出结论.
解:连接AD,OD,
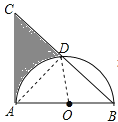
∵等腰直角△ABC中,
∴∠ABD=45°.
∵AB是圆的直径,
∴∠ADB=90°,
∴△ABD也是等腰直角三角形,
∴![]() .
.
∵AB=8,
∴AD=BD=4![]() ,
,
∴S阴影=S△ABCS△ABDS弓形AD=S△ABCS△ABD(S扇形AOD![]() S△ABD)
S△ABD)
=![]() ×8×8
×8×8![]() ×4
×4![]() ×4
×4![]()
![]() +
+![]() ×
×![]() ×4
×4![]() ×4
×4![]()
=32-164π+8
=244π.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
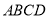 中,
中,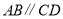 ,再添加下列其中一个条件后,四边形
,再添加下列其中一个条件后,四边形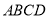 不一定是平行四边形的是( )
不一定是平行四边形的是( )A.
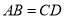 B.
B.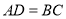 C.
C.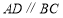 D.
D.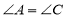
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和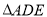 都是等边三角形,
都是等边三角形,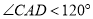 ,点
,点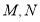 分别是
分别是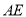 ,
, 的中点,连结
的中点,连结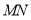 ,
,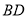 ,当
,当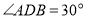 ,
,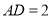 ,
,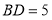 时,
时,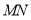 的长度为__________.
的长度为__________.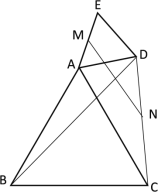
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
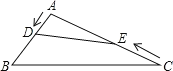
A. 4或4.8 B. 3或4.8 C. 2或4 D. 1或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一根固定长度的木棍
 在正方形
在正方形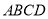 的内部如图1放置,此时木棍的端点
的内部如图1放置,此时木棍的端点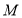 恰好与点
恰好与点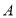 重合,点
重合,点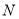 在
在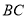 边上,
边上,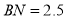 ,将木棍沿
,将木棍沿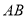 向下滑动
向下滑动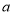 个单位长度至图2的位置.同时另一个端点
个单位长度至图2的位置.同时另一个端点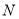 沿
沿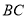 向右滑动
向右滑动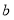 个单位长度至
个单位长度至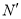 ,且
,且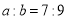 ,
,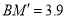 .在滑动的过程中,点
.在滑动的过程中,点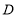 到木棍中点
到木棍中点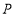 的最短距离为__________.
的最短距离为__________.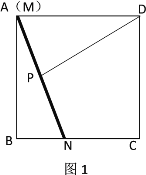
-
科目: 来源: 题型:
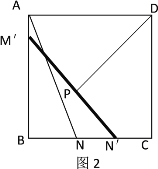
查看答案和解析>>【题目】学习完第五章《相交线与平行线》后,王老师布置了一道儿何证明题如下:“如图,已知直线AB,CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.”善于动脑的小军快速思考,找到了解题方案,并书写出了如下不完整的解题过程.请你将该题解题过程补充完整:
解:∵∠1=∠2=80°(已知)
∴AB∥CD
∴∠BGF+∠3=180°
∵∠2+∠EFD=180°(邻补角的定义),
∴∠EFD= °(等式性质)
∵FG平分∠EFD(已知),
∴∠EFD=2∠3(角平分线的定义)
∴∠3= °(等式性质)
∴∠BGF= °(等式性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
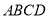 的边长为6个单位长度,点
的边长为6个单位长度,点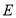 是
是 边的中点,点
边的中点,点 从点
从点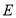 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按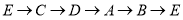 的方向运动,再次回到
的方向运动,再次回到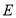 点结束运动,设
点结束运动,设 点运动的时间为
点运动的时间为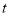 秒.
秒.

(1)如图1,若
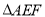 为直角三角形,求
为直角三角形,求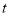 的值;
的值;(2)如图2,若点
 在
在 上,且
上,且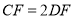 ,求
,求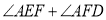 的度数;
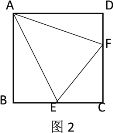
的度数;(3)如图3,点
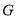 是对角线
是对角线 的三等分点,且
的三等分点,且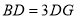 ,若
,若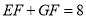 ,直接写出满足条件的
,直接写出满足条件的 点的个数,并注明这些
点的个数,并注明这些 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
相关试题

