【题目】如图,正方形![]() 的边长为6个单位长度,点
的边长为6个单位长度,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按![]() 的方向运动,再次回到
的方向运动,再次回到![]() 点结束运动,设
点结束运动,设![]() 点运动的时间为
点运动的时间为![]() 秒.
秒.


(1)如图1,若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
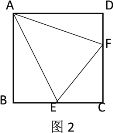
(2)如图2,若点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,点![]() 是对角线
是对角线![]() 的三等分点,且
的三等分点,且![]() ,若
,若![]() ,直接写出满足条件的
,直接写出满足条件的![]() 点的个数,并注明这些
点的个数,并注明这些![]() 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
参考答案:
【答案】(1)4.5或12或21;(2)135°;(3)有两个,分别在![]() 和
和![]() 上
上
【解析】
(1)分当点F在CD上、AD上以及和点B重合时三种情况分别求出相应的t值;
(2)根据题意求出DF和CF,EF,延长![]() 至点
至点![]() ,证明
,证明![]() ,得到
,得到![]() ,
,![]() ,再证明
,再证明![]() ,得到对应角相等,最后根据
,得到对应角相等,最后根据![]() 可得结果;
可得结果;
(3)分点F在正方形各边上的情况,分别求出![]() 的最值,即可得出结果.
的最值,即可得出结果.
解:(1)①当点![]() 在
在![]() 上,
上,![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
解之:![]() ,
,
②当点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
③当点![]() 与
与![]() 点重合,
点重合,![]() ,
,![]() ,
,
(2)解:∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
延长![]() 至点
至点![]() ,使
,使![]() ,
,
则![]() ,
,
在![]() 与
与![]() 中,
中,
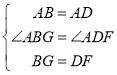 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
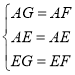 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ;
;
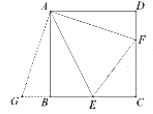
(3)满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 边和
边和![]() 上.
上.
理由是:当点F在AB上时,如图,
E′为点E关于AB的对称点,GH⊥BC于H,
∵GH∥CD,
∴![]() ,
,
可得GH=BH=4,
∴![]() 的最小值为E′G=
的最小值为E′G=![]() >8,
>8,
即AB上没有符合要求的F;
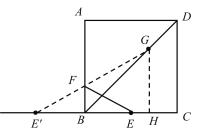
当点F在AD上时,如图,
E′为点E关于AD的对称点,
同理可得:KG=![]() AB=2,HG=6+2=8<E′G,
AB=2,HG=6+2=8<E′G,
∴此时![]() 的最小值为E′G的长,大于8,
的最小值为E′G的长,大于8,
∴AD上不存在符合要求的F;

当点F在CD上时,如图,
E′为点E关于CD的对称点,GH⊥BC于H,
同理可得:GH=BH=4,HC=2,
∴HE′=5,
此时![]() 的最小值为E′G=
的最小值为E′G=![]() <8,
<8,
当点F在点D处时,![]() =ED+GD=
=ED+GD=![]() =
=![]() ,
,
∴CD上存在符合要求的点F;
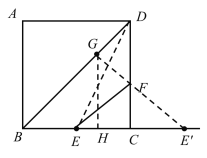
当点F在BC上时,GH⊥BC于H,
若点F与点E重合,
同理可知GH=4=BH,EH=BH-BE=1,
则![]() =GE=
=GE=![]() <8,
<8,
若点F与点B重合,
同理可知BG=![]() ,BE=3,
,BE=3,
则![]() =BE+BG=
=BE+BG=![]() =8,
=8,
故BC上存在符合要求的点F;
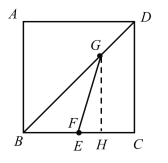
综上:满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 和
和![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
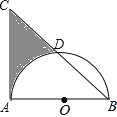
A. 16 B. 24-4π C. 32-4π D. 32-8π
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一根固定长度的木棍
 在正方形
在正方形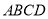 的内部如图1放置,此时木棍的端点
的内部如图1放置,此时木棍的端点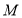 恰好与点
恰好与点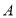 重合,点
重合,点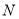 在
在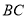 边上,
边上,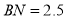 ,将木棍沿
,将木棍沿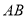 向下滑动
向下滑动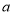 个单位长度至图2的位置.同时另一个端点
个单位长度至图2的位置.同时另一个端点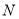 沿
沿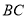 向右滑动
向右滑动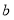 个单位长度至
个单位长度至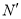 ,且
,且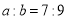 ,
,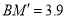 .在滑动的过程中,点
.在滑动的过程中,点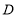 到木棍中点
到木棍中点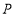 的最短距离为__________.
的最短距离为__________.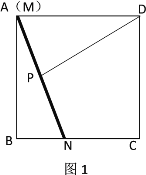
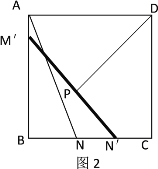
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习完第五章《相交线与平行线》后,王老师布置了一道儿何证明题如下:“如图,已知直线AB,CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.”善于动脑的小军快速思考,找到了解题方案,并书写出了如下不完整的解题过程.请你将该题解题过程补充完整:
解:∵∠1=∠2=80°(已知)
∴AB∥CD
∴∠BGF+∠3=180°
∵∠2+∠EFD=180°(邻补角的定义),
∴∠EFD= °(等式性质)
∵FG平分∠EFD(已知),
∴∠EFD=2∠3(角平分线的定义)
∴∠3= °(等式性质)
∴∠BGF= °(等式性质)
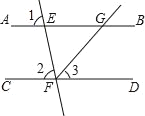
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'
(1)在图中画出△A′B′C';
(2)写出A',B'的坐标;
(3)求出△COC′的面积;
(4)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
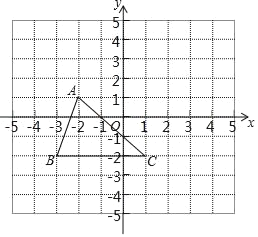
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成相应的任务.
我们知道,二元一次方程有无数个解.在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如:
 ,方程x﹣y=﹣1的一个解,对应点为(1,2).
,方程x﹣y=﹣1的一个解,对应点为(1,2).我们在平面直角坐标系中标出,另外方程x﹣y=﹣1的解还对应点(2,3),(3,4)…将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程x﹣1=﹣1的解,所以,我们就把这条直线叫做方程x﹣y=﹣1的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.那么每个二元一次方程组应该对应两条直线,解这个方程组,相当于确定两条直线交点的坐标.
(1)已知A(1,1),B(﹣3,4),C(,2),则点 (填“A”、”B”、“C”)在方程2x﹣y=﹣1的图象上;
(2)求方程2x+3y=9和方程3x﹣4y=5图象的交点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.

小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
相关试题

