【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
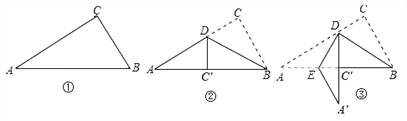
A. 3cm B. 4cm C. 5cm D. 6cm
参考答案:
【答案】B
【解析】分析:先根据在一个直角三角形纸片,∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,所以∠BDE=90°,在Rt△BDE中, ∠DBE=30°,DE=![]() ,根据30°角所对直角边等于斜边的一半,可得:BE=
,根据30°角所对直角边等于斜边的一半,可得:BE=![]() ,根据勾股定理可得:BD=
,根据勾股定理可得:BD=![]() , 在Rt△DBC中, ∠DBC=30°,DB=
, 在Rt△DBC中, ∠DBC=30°,DB=![]() ,根据30°角所对直角边等于斜边的一半,可得:DC=
,根据30°角所对直角边等于斜边的一半,可得:DC=![]() ,根据勾股定理可得:BC=
,根据勾股定理可得:BC=![]() .
.
详解: 因为∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,
所以∠BDE=90°,
在Rt△BDE中, 因为∠DBE=30°,DE=![]() ,
,
所以BE=![]() ,
,
根据勾股定理可得:BD=![]() ,
,
在Rt△DBC中, ∠DBC=30°,DB=![]() ,根
,根
所以DC=![]() ,
,
根据勾股定理可得:BC=![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
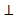
(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年9月11日,以“绿色生活从你我做起”为主题的重庆市第四届生态文明知识竞赛活动正式启动.某校组织全校学生参与后,王老师抽取了班上第一大组8名学生的成绩,若以80分为标准,超过的分数用正数表示,不足的分数用负数表示,成绩记录如下:﹣3,+7,﹣12,+18,+6,﹣5,﹣21,+14
(1)最高分比最低分多多少分?第一大组平均每人得多少分?
(2)若规定:成绩高于80分的学生操行分每人加3分,成绩在60~80分的学生操行分每人加2分,成绩在60分以下的学生操行分每人扣1分,那么第一大组的学生共加操行分多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )
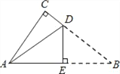
A. 1.75 B. 3 C. 3.75 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
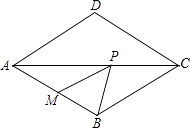
A.6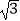
B.3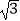
C.9
D.4.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y= 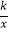 (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= 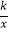 (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
相关试题

