【题目】类比学习:一动点沿着数轴向右平移3个单位,再向左平移![]() 个单位,相当于向右平移1个单位.用实数加法表示为
个单位,相当于向右平移1个单位.用实数加法表示为 ![]() .
.
若坐标平面上的点作如下平移:沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向右为正,向左为负,平移
(向右为正,向左为负,平移![]() 个单位),沿
个单位),沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向上为正,向下为负,平移
(向上为正,向下为负,平移![]() 个单位),则把有序数对{
个单位),则把有序数对{![]() ,
,![]() }叫做这一平移的“平移量”;“平移量”{
}叫做这一平移的“平移量”;“平移量”{![]() ,
,![]() }与“平移量”{
}与“平移量”{![]() ,
,![]() }的加法运算法则为
}的加法运算法则为![]() .
.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图中画出四边形OABC.
②证明四边形OABC是平行四边形.
参考答案:
【答案】(1){4,3};{4,3};(2)①最后的位置仍是B,图见解析;②见解析.
【解析】
(1)本题主要是类比学习,所以关键是由给出的例题中找出解题规律,即前项加前项,后项加后项.
(2)根据题中给出的平移量找出各对应点,描出各点,顺次连接即可.
(1){3,1}+{1,2}={4,3};
{1,2}+{3,1}={4,3}.
(2)①画图
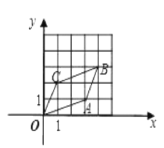
最后的位置仍是B.
②证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB=![]() ,
,
OA=BC=![]() ,
,
∴四边形OABC是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
(2)如图,AB是
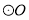 的直径,PA与
的直径,PA与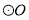 相切于点A,OP与
相切于点A,OP与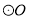 相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.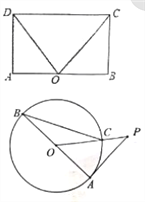
-
科目: 来源: 题型:
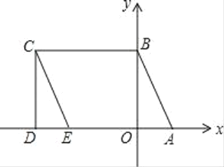
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
(1)直接写出点E的坐标 ;D的坐标
(3)点P是线段CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x, y,z之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
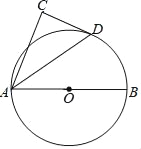
查看答案和解析>>【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学活动课上,将边长为
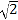 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
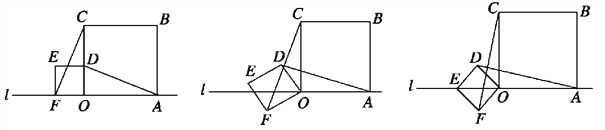
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型
价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?
相关试题

