【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, ![]() .
.

(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
参考答案:
【答案】
【1】D(0,2)
【2】![]()
![]()
【3】![]()
【解析】这道题是一道综合体,其中一次函数,二次函数,相似三角形都有涉及。
【1】分析:求点D的坐标就要知道OD的长度就可以了,怎么求OD长度呢?由题意,我们知道![]() 与Y轴交与D点,所以点D的坐标为(0,2)。
与Y轴交与D点,所以点D的坐标为(0,2)。
【2】分析:求一次函数与反比例函数的解析式,分析题意可知道如果能求出这两个函数图像的交点P的坐标,然后代入解析式,分别求出m和k的值。
【3】根据图像,可知取原点右边和A点左边就是x的取值范围。
-
科目: 来源: 题型:
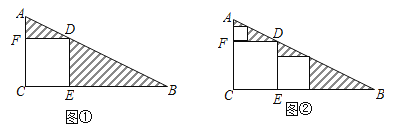
查看答案和解析>>【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求
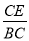 和S1的值;
和S1的值;(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的表达式;
(2)若直线AB上有一动点C,且
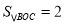 ,求点C的坐标.
,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于E.
(1)求∠AEC的度数;
(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF⊥AB,CD⊥AB,下列说法:①EF∥CD;②∠B+∠BDG=180°;③若∠1=∠2,则∠1=∠BEF;④若∠ADG=∠B,则∠DGC+∠ACB=180°,其中说法正确的是( )
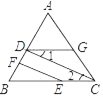
A. ①②B. ③④C. ①②③D. ①③④
-
科目: 来源: 题型:
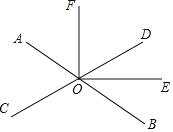
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
相关试题

