搜索
【题目】如图，在平面直角坐标系中，△ABC的顶点A，B在反比例函数
的图象上，横坐标分别为1、3.5，AB＝AC,BC与
轴平行，若△ABC的面积为
，则
的值为（ ）
A. 
B. 5
C. 
D. 
参考答案：
【答案】A
【解析】
根据题意，利用面积法求出AE，设出点B坐标，表示点A的坐标．应用反比例函数上点的横纵坐标乘积为k求解即可．
连接过点A作AF⊥x轴，垂足为F，交BC于点E．
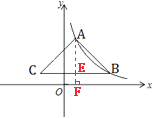
由已知，A、B横坐标分别为1，3.5
∴BE=2.5
∵AB=AC，BC∥x轴，
∴AE⊥BC，CE=BE=2.5
∴BC=5，
∵S△ABC=
×5×AE =
∴AE=3
设点B的坐标为（3.5，y），则A点坐标为（1，y+3）
∵点A、B同在y=
图象上
∴3.5y=1×（y+3）
∴y=
∴B点坐标为（3.5，）
∴k=
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
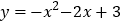的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）.若FG=
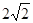DQ，求点F的坐标.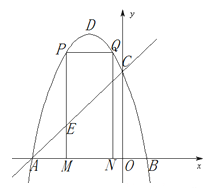
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在△ABC中，AB=BC=4，∠ABC=90°，M是AC的中点，点N在AB上（不同于A、B），将△ANM绕点M逆时针旋转90°得△A1PM.
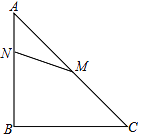
（1）画出△A1PM
（2）设AN=x，四边形NMCP的面积为y，直接写出y关于x的函数关系式，并求y的最大或最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
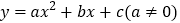与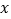
轴交于A（－1，0），B（3，0）两点，与
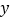轴交于点C，顶点为D，下列结论正确的是（ ）
A. abc＜0 B. 3a+c=0 C. 4a-2b+c＜0 D. 方程ax2+bx+c=-2（a≠0）有两个不相等的实数根
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，点E是CD的中点，连接BE并延长交AD延长线于点F．
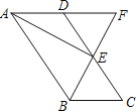
（1）求证：点D是AF的中点；
（2）若AB=2BC，连接AE，试判断AE与BF的位置关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，AB＜AD，∠D=30°，CD=4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书，第一次用500元购书若干本，很快售完由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用900元所购该书的数量比第一次的数量多了10本．
（1）求第一次购书每本多少元？
（2）如果这两次所购图书的售价相同，且全部售完后总利润不低于25%，那么每本图书的售价至少是多少元？
相关试题
