【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
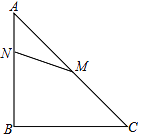
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
参考答案:
【答案】(1)见解析;(2)y=![]() (x﹣3)2+
(x﹣3)2+ ![]() ,最小值为
,最小值为![]() .
.
【解析】
(1)根据旋转的定义,画出旋转90°的△A1PM即可;
(2)过点M作MD⊥AB于点D,用割补法表示出四边形NMCP的面积y,化为顶点式,根据二次函数的性质求解即可.
(1)解:如图所示:△A1PM,即为所求;
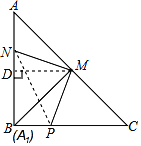
(2)解:过点M作MD⊥AB于点D,
∵AB=BC=4,∠ABC=90°,M是AC的中点,
∴MD=2,
设AN=x,则BN=4﹣x,
故四边形NMCP的面积为:
y= ![]() ×4×4﹣
×4×4﹣ ![]() x×2﹣
x×2﹣ ![]() x×(4﹣x)
x×(4﹣x)
= ![]() x2﹣3x+8
x2﹣3x+8
= ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
故y的最小值为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
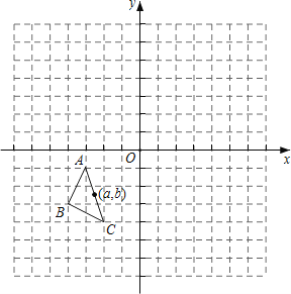
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
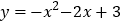 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=
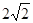 DQ,求点F的坐标.
DQ,求点F的坐标.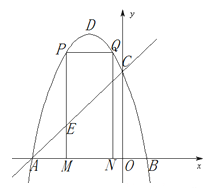
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
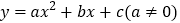 与
与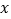 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与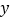 轴交于点C,顶点为D,下列结论正确的是( )
轴交于点C,顶点为D,下列结论正确的是( )
A. abc<0 B. 3a+c=0 C. 4a-2b+c<0 D. 方程ax2+bx+c=-2(a≠0)有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点A,B在反比例函数
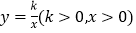 的图象上,横坐标分别为1、3.5,AB=AC,BC与
的图象上,横坐标分别为1、3.5,AB=AC,BC与 轴平行,若△ABC的面积为
轴平行,若△ABC的面积为 ,则
,则 的值为( )
的值为( )
A.
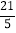 B. 5
B. 5C.
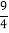 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是CD的中点,连接BE并延长交AD延长线于点F.
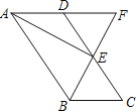
(1)求证:点D是AF的中点;
(2)若AB=2BC,连接AE,试判断AE与BF的位置关系,并说明理由.
相关试题

