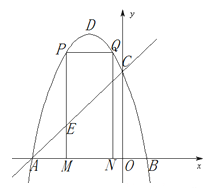
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.
参考答案:
【答案】(1)A(-3,0),B(1,0),C(0,3); (2)![]() ;(3)
;(3)![]() 或(1,0).
或(1,0).
【解析】
试题(1)通过解析式即可得出C点坐标,令y=0,解方程得出方程的解,即可求得A、B的坐标;
(2)设M点横坐标为m,则PM=![]() ,MN=(﹣m﹣1)×2=﹣2m﹣2,矩形PMNQ的周长d=
,MN=(﹣m﹣1)×2=﹣2m﹣2,矩形PMNQ的周长d=![]() ,将
,将![]() 配方,由二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积;
配方,由二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积;
(3)设F(n,![]() ),由已知若FG=
),由已知若FG=![]() DQ,即可求得.
DQ,即可求得.
试题解析:解:(1)由抛物线![]() 可知,C(0,3),令y=0,则
可知,C(0,3),令y=0,则![]() ,解得x=﹣3或x=1,∴A(﹣3,0),B(1,0);
,解得x=﹣3或x=1,∴A(﹣3,0),B(1,0);
(2)由抛物线![]() 可知,对称轴为x=﹣1,设M点的横坐标为m,则PM=
可知,对称轴为x=﹣1,设M点的横坐标为m,则PM=![]() ,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(
,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(![]() )×2=
)×2=![]() =
=![]() ,∴当m=﹣2时矩形的周长最大.∵A(﹣3,0),C(0,3),设直线AC解析式为y=kx+b,解得k=1,b=3,∴解析式y=x+3,当x=﹣2时,则E(﹣2,1),∴EM=1,AM=1,∴S=
,∴当m=﹣2时矩形的周长最大.∵A(﹣3,0),C(0,3),设直线AC解析式为y=kx+b,解得k=1,b=3,∴解析式y=x+3,当x=﹣2时,则E(﹣2,1),∴EM=1,AM=1,∴S=![]() AMEM=
AMEM=![]() ;
;
(3)∵M点的横坐标为﹣2,抛物线的对称轴为x=﹣1,∴N应与原点重合,Q点与C点重合,∴DQ=DC,把x=﹣1代入![]() ,解得y=4,∴D(﹣1,4),∴DQ=DC=
,解得y=4,∴D(﹣1,4),∴DQ=DC=![]() ,∵FG=
,∵FG=![]() DQ,∴FG=4,设F(n,
DQ,∴FG=4,设F(n,![]() ),则G(n,n+3),∵点G在点F的上方,∴
),则G(n,n+3),∵点G在点F的上方,∴![]() =4,解得:n=﹣4或n=1,∴F(﹣4,﹣5)或(1,0).
=4,解得:n=﹣4或n=1,∴F(﹣4,﹣5)或(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
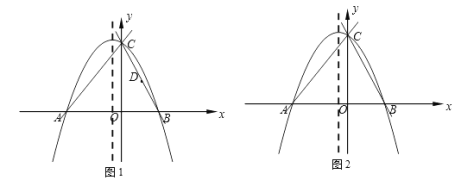
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线y=ax+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
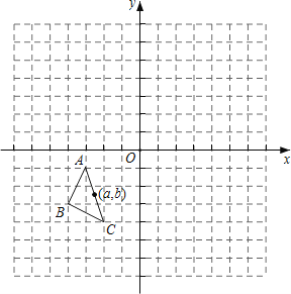
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
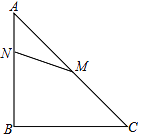
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
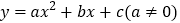 与
与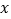 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与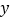 轴交于点C,顶点为D,下列结论正确的是( )
轴交于点C,顶点为D,下列结论正确的是( )
A. abc<0 B. 3a+c=0 C. 4a-2b+c<0 D. 方程ax2+bx+c=-2(a≠0)有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点A,B在反比例函数
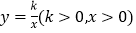 的图象上,横坐标分别为1、3.5,AB=AC,BC与
的图象上,横坐标分别为1、3.5,AB=AC,BC与 轴平行,若△ABC的面积为
轴平行,若△ABC的面积为 ,则
,则 的值为( )
的值为( )
A.
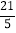 B. 5
B. 5C.
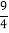 D.
D. 
相关试题

