【题目】如下图。 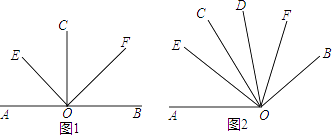
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
参考答案:
【答案】
(1)解:∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC= ![]() ∠AOC=
∠AOC= ![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°
(2)解:∵OE平分∠AOD,
∴∠EOD= ![]() ∠AOD=
∠AOD= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∠COE=∠EOD﹣∠COD=40+ ![]() β﹣β=40﹣
β﹣β=40﹣ ![]() β;
β;
∠EOF=∠COE+∠COF=40﹣ ![]() β+40+
β+40+ ![]() β=80°
β=80°
(3)![]()
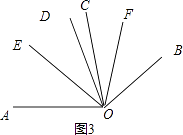
【解析】解:(3)如图2,∵∠AOC=∠BOD=α,∠COD=β, ∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD= ![]() =
= ![]() ,
,
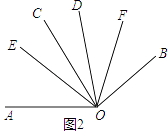
如图3,∵∠AOC=∠BOD=α,∠COD=β,
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD= ![]() .
.
综上所述: ![]() ,
,
故答案为: ![]() .
.
(1)根据垂直的定义得到∠AOC=∠OC=90°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义得到∠EOD= ![]() ∠AOD=
∠AOD= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,∠COF=
β,∠COF= ![]() ∠BOC=
∠BOC= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=
β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE= ![]() (α+β),即可得到结论.
(α+β),即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△DEF , 若∠A=50°,∠B=60°,则∠F的度数是( )
A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】若4a+3b=1,则8a+6b-3的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A,B,C都在格点上.

(1)过点C画直线AB的平行线(仅利用所给方格纸和直尺作图,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段的长度是点A到直线BC的距离;线段AH的长度是点H到直线的距离.
(4)线段AG、AH的大小关系为:AGAH.理由: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】n边形的外角和是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的相反数是负数,那么这个数一定是( ).
A.正数
B.负数
C.零
D.正数、负数、零都有可能
相关试题

