【题目】“五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.
(1)顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.
(2)请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率.
参考答案:
【答案】
(1)0,60
(2)解:画树状图如下:
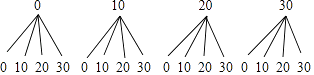
共16种情况,不低于30元的情况数有10种,
所以所求的概率为 ![]() =
= ![]()
【解析】(1)至少得到的金额数为0+0=0元,至多得到的金额数为30+30=60元,
(2)画树状图如下:

共16种情况,不低于30元的情况数有10种,
所以所求的概率为 ![]() =
= ![]() .
.
所以答案是:(1)0、60;(2)![]() .
.
【考点精析】掌握列表法与树状图法是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
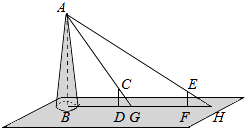
查看答案和解析>>【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 ,直线
,直线 与直线
与直线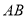 、
、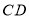 分别相交于点
分别相交于点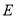 、
、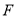 .
.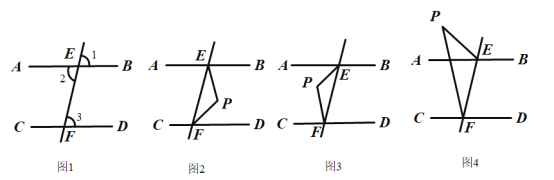
(1)如图1,若
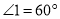 ,求
,求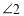 ,
,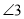 的度数;
的度数;(2)若点
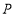 是平面内的一个动点,连接
是平面内的一个动点,连接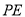 、
、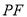 ,探索
,探索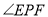 、
、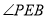 、
、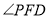 之间的数量关系;
之间的数量关系;①当点
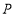 在图2的位置时,请写出
在图2的位置时,请写出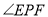 、
、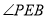 、
、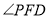 之间的数量关系并证明;
之间的数量关系并证明;②当点
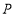 在图3的位置时,请写出
在图3的位置时,请写出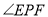 、
、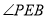 、
、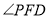 之间的数量关系并证明;
之间的数量关系并证明;③当点
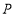 在图4的位置时,请直接写出
在图4的位置时,请直接写出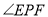 、
、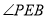 、
、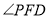 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.
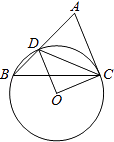
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探究:12=
 ,12+22=
,12+22= ,12+22+32=
,12+22+32=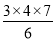 ,…
,…(1)根据上述规律,求12+22+32+42+52的值;
(2)你能用一个含有n(n为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算);
(3)根据你发现的规律,计算下面算式的值:62+72+82+92+102+112+122+132+142+152.
相关试题

