【题目】已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
参考答案:
【答案】解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,
方程3x2+2x﹣1=0的两个根为x1=﹣1, ![]() .
.
∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ![]() ,0);
,0);
(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.
对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ ![]() .
.
①当 ![]() 时,由方程3x2+2x+
时,由方程3x2+2x+ ![]() =0,解得x1=x2=﹣
=0,解得x1=x2=﹣ ![]() .
.
此时抛物线为y=3x2+2x+ ![]() 与x轴只有一个公共点(﹣
与x轴只有一个公共点(﹣ ![]() ,0);
,0);
②当 ![]() 时,x1=﹣1时,y1=3﹣2+c=1+c;
时,x1=﹣1时,y1=3﹣2+c=1+c;
x2=1时,y2=3+2+c=5+c.
由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ![]() ,
,
应有 ![]() 即
即 ![]() ,
,
解得﹣5<c≤﹣1.
综上, ![]() 或﹣5<c≤﹣1.(6分)
或﹣5<c≤﹣1.(6分)
(Ⅲ)对于二次函数y=3ax2+2bx+c,
由已知x1=0时,y1=c>0;
x2=1时,y2=3a+2b+c>0,
又∵a+b+c=0,
∴3a+2b+c=(a+b+c)+2a+b=2a+b.
∴2a+b>0.
∵b=﹣a﹣c,
∴2a﹣a﹣c>0,即a﹣c>0.
∴a>c>0.(7分)
∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,
∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.
又该抛物线的对称轴 ![]() ,
,
由a+b+c=0,c>0,2a+b>0,
得﹣2a<b<﹣a,
∴ ![]() .
.
又由已知x1=0时,y1>0;
x2=1时,y2>0,观察图象, 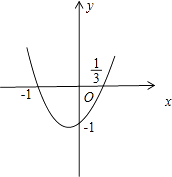
可知在0<x<1范围内,该抛物线与x轴有两个公共点.
【解析】(Ⅰ)把a,b,c的值代入可得抛物线的解析式,然后令y=0可得到关于x的方程,然后求得方程的两根,从而可得到抛物线与x轴交点坐标;
(Ⅱ)把a,b代入可得到抛物线的解析式,然后可求得抛物线的对称轴为x=-![]() ,然后再分为△=0和△>0两种情况求解即可;
,然后再分为△=0和△>0两种情况求解即可;
(Ⅲ)抛物线y=3ax2+2bx+c与x轴公共点的个数就是一元二次方程3ax2+2bx+c=0的实数根的个数,接下来,判断出方程3ax2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.
(1)顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.
(2)请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.
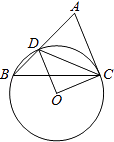
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探究:12=
 ,12+22=
,12+22= ,12+22+32=
,12+22+32=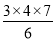 ,…
,…(1)根据上述规律,求12+22+32+42+52的值;
(2)你能用一个含有n(n为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算);
(3)根据你发现的规律,计算下面算式的值:62+72+82+92+102+112+122+132+142+152.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究
(1)请在图①的正方形ABCD的对角线BD上作一点P,使PA+PC最小;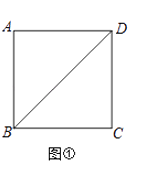
(2)如图②,点P为矩形ABCD的对角线BD上一动点,AB=2,BC=2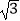 ,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.
,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.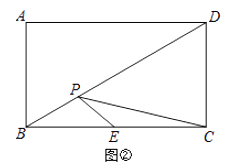
(3)如图③,李师傅有一块边长为1000米的菱形ABCD采摘园,AC=1200米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出的点P位置,并求出这个最短距离;若不存在,请说明理由.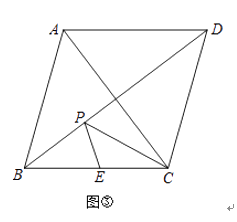
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
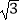 的线段的概率为( )
的线段的概率为( )
A.
B.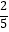
C.
D.
相关试题

