【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
参考答案:
【答案】(1)8;(2)|x-3|(或填|3-x|);(3)6;![]() ;(4)x<4或x>2.
;(4)x<4或x>2.
【解析】
(1)根据两点间的距离公式即可求解;
(2)根据两点间的距离公式可求A与B两点的距离;
(3)|x+4|即x与4的差的绝对值,它可以表示数轴上x与4之间的距离.|x2|即x与2的差的绝对值,它也可以表示数轴上x与2之间的距离.借助数轴,我们可以得到正确答案;
(4)借助数轴,我们可以得到正确答案:x<4或x>2.
解:(1)A与B两点间的距离是|6(2)|=8.
故答案为:8;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点的距离可以表示为|x3|或|3-x|,
故答案为:|x3|或|3-x|;
(3)如图:|x+4|表示数轴上表示x的点与4之间的距离,|x2|表示数轴上表示x的点与2之间的距离,若|x+4|+|x2|的值最小,x应在数轴上4与2之间,因此最小值为6,
答:|x+4|+|x2|的最小值为6,取得最小值时x的取值范围为4≤x≤2;
故答案为6,4≤x≤2;

(4)借助数轴分析,可以得到满足|x+4|+|x2|>6的x的取值范围为:x<4或x>2,
故答案为:x<4或x>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气象站观察一场沙尘暴从发生到结束的全过程,开始时风速按一定的速度匀速增大,经过荒漠地时,风速增大的比较快.一段时间后,风速保持不变,当沙尘暴经过防风林时,其风速开始逐渐减小,最终停止.如图所示是风速与时间之间的关系的图象.结合图象回答下列问题:

(1)沙尘暴从开始发生到结束共经历了多长时间?
(2)从图象上看,风速在哪一个时间段增大的比较快,增加的速度是多少?
(3)风速在哪一时间段保持不变,经历了多长时间?
(4)风速从开始减小到最终停止,风速每小时减小多少?
-
科目: 来源: 题型:
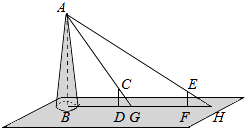
查看答案和解析>>【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
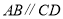 ,直线
,直线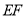 与直线
与直线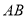 、
、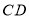 分别相交于点
分别相交于点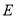 、
、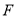 .
.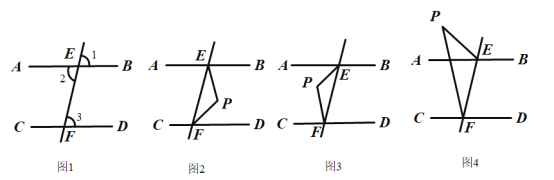
(1)如图1,若
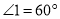 ,求
,求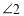 ,
,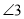 的度数;
的度数;(2)若点
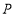 是平面内的一个动点,连接
是平面内的一个动点,连接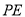 、
、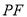 ,探索
,探索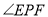 、
、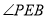 、
、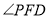 之间的数量关系;
之间的数量关系;①当点
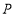 在图2的位置时,请写出
在图2的位置时,请写出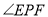 、
、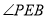 、
、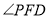 之间的数量关系并证明;
之间的数量关系并证明;②当点
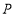 在图3的位置时,请写出
在图3的位置时,请写出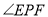 、
、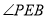 、
、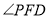 之间的数量关系并证明;
之间的数量关系并证明;③当点
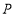 在图4的位置时,请直接写出
在图4的位置时,请直接写出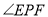 、
、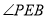 、
、 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.
(1)顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.
(2)请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.
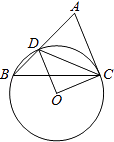
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
相关试题

