【题目】如图,已知 A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请在图中作出△ABC 关于 y 轴对称的△![]() ,并求出△
,并求出△![]() 的面积;
的面积;
(2)写出 ![]() 、
、![]() 的坐标
的坐标 ![]() __________;
__________;![]() __________;
__________;
(3)若△DBC 与△ABC 全等,则 D 的坐标为_____.
参考答案:
【答案】(1)作图见详解;7.5;(2) (2,3),(6,0);(3) (﹣2,﹣3)或(﹣5,﹣3)或(-5,3).
【解析】
(1)根据关于y轴对称的点的坐标变化特点可得![]() 、
、![]() 、
、![]() 的坐标,再连接即可.
的坐标,再连接即可.
(2)根据关于y轴对称的点的坐标变化特点可得![]() ,
, ![]() 的坐标;
的坐标;
(3)由全等三角形的判定方法容易得出结果.
解:(1)如图所示,△![]() 即为所求.
即为所求.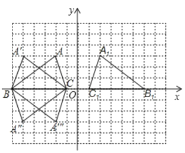
![]() 的面积为
的面积为 ![]() ×5×3=7.5;
×5×3=7.5;
(2)由图知,![]() 的坐标为(2,3),
的坐标为(2,3),![]() 的坐标为(6,0),故答案为:(2,3),(6,0).
的坐标为(6,0),故答案为:(2,3),(6,0).
(3)如图,D 的坐标为(﹣2,﹣3)或(﹣5,﹣3)或(-5,3),故答案为:(﹣2,﹣3)或(﹣5,﹣3)或(-5,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+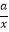 )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+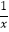 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+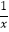 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.x
…



1
2
3
m
…
y
…
4

3

2

2
2

3

4

…
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.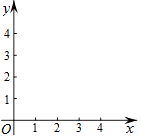
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+2m﹣1(m≠0)与平行于x轴的一条直线交于A,B两点.

(1)求抛物线的对称轴;
(2)如果点A的坐标是(﹣1,﹣2),求点B的坐标;
(3)抛物线的对称轴交直线AB于点C,如果直线AB与y轴交点的纵坐标为﹣1,且抛物线顶点D到点C的距离大于2,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C 是路段 AB 的中点,两人从 C 同时出发,以相同的速度分别沿两条直线行走,并同时到达 D,E 两地,DA⊥AB,EB⊥AB,D,E 与路段AB 的距离相等吗?为什么?
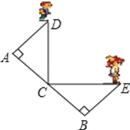
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E 是 BC 的中点,DE 平分∠ADC.
(1)如图 1,若∠B=∠C=90°,求证:AE 平分∠DAB;
(2)如图 2,若 DE⊥AE,求证:AD=AB+CD.
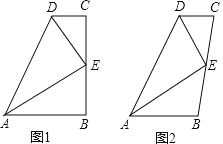
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
-
科目: 来源: 题型:
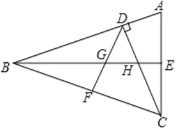
查看答案和解析>>【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
相关试题

