【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+2m﹣1(m≠0)与平行于x轴的一条直线交于A,B两点. 
(1)求抛物线的对称轴;
(2)如果点A的坐标是(﹣1,﹣2),求点B的坐标;
(3)抛物线的对称轴交直线AB于点C,如果直线AB与y轴交点的纵坐标为﹣1,且抛物线顶点D到点C的距离大于2,求m的取值范围.
参考答案:
【答案】
(1)解:(1)∵抛物线y=mx2﹣4mx+2m﹣1=m(x﹣2)2﹣2m﹣1,
∴对称轴为x=2
(2)∵抛物线是轴对称图形,
∴点A点B关于x=2轴对称,
∵A(﹣1,﹣2),
∴B(5,﹣2).
(3)∵抛物线y=mx2﹣4mx+2m﹣1=m(x﹣2)2﹣2m﹣1,
∴顶点D(2,﹣2m﹣1).
∵直线AB与y轴交点的纵坐标为﹣1,
∴C(2,﹣1).
∵顶点D到点C的距离大于2,
∴﹣2m﹣1+1>2或﹣1+2m+1>2,
∴m<﹣1或m>1.
【解析】(1)化成顶点式即可求得;(2)根据轴对称的特点求得即可;(3)求得顶点坐标,根据题意求得C的坐标,分两种情况表示出顶点D到点C的距离,列出不等式,解不等式即可求得.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
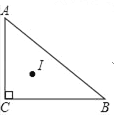
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+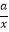 )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+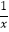 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+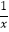 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.x
…



1
2
3
m
…
y
…
4

3

2

2
2

3

4

…
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.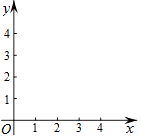
-
科目: 来源: 题型:
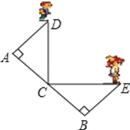
查看答案和解析>>【题目】如图,C 是路段 AB 的中点,两人从 C 同时出发,以相同的速度分别沿两条直线行走,并同时到达 D,E 两地,DA⊥AB,EB⊥AB,D,E 与路段AB 的距离相等吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请在图中作出△ABC 关于 y 轴对称的△
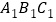 ,并求出△
,并求出△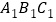 的面积;
的面积;(2)写出
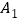 、
、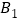 的坐标
的坐标 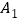 __________;
__________;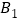 __________;
__________;(3)若△DBC 与△ABC 全等,则 D 的坐标为_____.
-
科目: 来源: 题型:
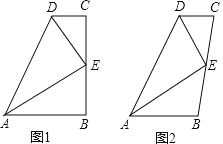
查看答案和解析>>【题目】如图,E 是 BC 的中点,DE 平分∠ADC.
(1)如图 1,若∠B=∠C=90°,求证:AE 平分∠DAB;
(2)如图 2,若 DE⊥AE,求证:AD=AB+CD.
相关试题

