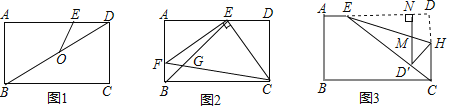
【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求![]() 的值;
的值;
②连接BE,△D'MH与△CBE是否相似?请说明理由.
参考答案:
【答案】(1)AE=![]() ;(2)BG=
;(2)BG=![]() ;(3)①
;(3)①![]() ;②相似,理由见解析.
;②相似,理由见解析.
【解析】
(1)先求出BD,进而求出OD=OB=OA,再判断出△ODE∽△ADO,即可得出结论;
(2)先判断出△AEF≌△DCE,进而求出BF=1,再判断出△CHG∽△CBF,进而求出BK=GK=![]() ,最后用勾股定理即可得出结论;
,最后用勾股定理即可得出结论;
(3)①先求出EC=5,再求出D'C=1,根据勾股定理求出DH=![]() ,CH=
,CH=![]() ,再判断出△EMN∽△EHD,得出
,再判断出△EMN∽△EHD,得出![]() ,△ED'M∽△ECH,得出
,△ED'M∽△ECH,得出![]() ,进而得出
,进而得出![]() ,即可得出结论;
,即可得出结论;
②先判断出∠MD'H=∠NED',进而判断出∠MD'H=∠ECB,即可得出![]() ,即可.
,即可.
(1)如图1,连接OA,
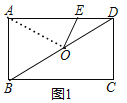
在矩形ABCD中,CD=AB=3,AD=BC=5,∠BAD=90°
在Rt△ABD中,根据勾股定理得,BD=![]() ,
,
∵O是BD中点,
∴OD=OB=OA=![]() ,
,
∴∠OAD=∠ODA,
∵OE=DE,
∴∠EOD=∠ODE,
∴∠EOD=∠ODE=∠OAD,
∴△ODE∽△ADO,
∴![]() ,
,
∴DO2=DEDA,
∴设AE=x,
∴DE=5﹣x,
∴(![]() )2=5(5﹣x),
)2=5(5﹣x),
∴x=![]() ,
,
即:AE=![]() ;
;
(2)如图2,
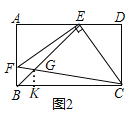
在矩形ABCD中,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴AE=CD=3,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠CED=90°,
∵∠A=90°,
∴∠AEF+∠AFE=90°,
∴∠CED=∠AFE,
∵∠D=∠A=90°,
∴△AEF≌△DCE,
∴AF=DE=2,
∴BF=AB﹣AF=1,
过点G作GK⊥BC于K,
∴∠EBC=∠BGK=45°,
∴BK=GK,∠ABC=∠GKC=90°,
∵∠KCG=∠BCF,
∴△CHG∽△CBF,
∴![]() ,
,
设BK=GK=y,
∴CK=5﹣y,
∴y=![]() ,
,
∴BK=GK=![]() ,
,
在Rt△GKB中,BG=![]() ;
;
(3)①在矩形ABCD中,∠D=90°,
∵AE=1,AD=5,
∴DE=4,
∵DC=3,
∴EC=5,
由折叠知,ED'=ED=4,D'H=DH,∠ED'H=∠D=90°,
∴D'C=1,
设D'H=DH=z,
∴HC=3﹣z,
根据勾股定理得,(3﹣z)2=1+z2,
∴z=![]() ,
,
∴DH=![]() ,CH=
,CH=![]() ,
,
∵D'N⊥AD,
∴∠AND'=∠D=90°,
∴D'N∥DC,
∴△EMN∽△EHD,
∴![]() ,
,
∵D'N∥DC,
∴∠ED'M=∠ECH,
∵∠MED'=∠HEC,
∴△ED'M∽△ECH,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②相似,理由:由折叠知,∠EHD'=∠EHD,∠ED'H=∠D=90°,
∴∠MD'H+∠ED'N=90°,
∵∠END'=90°,
∴∠ED'N+∠NED'=90°,
∴∠MD'H=∠NED',
∵D'N∥DC,
∴∠EHD=∠D'MH,
∴∠EHD'=∠D'MH,
∴D'M=D'H,
∵AD∥BC,
∴∠NED'=∠ECB,
∴∠MD'H=∠ECB,
∵CE=CB=5,
∴![]()
∴△D'MH∽△CBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为
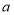 ,
,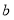 的矩形发生形变后成为边长为
的矩形发生形变后成为边长为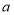 ,
,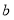 的平行四边形,如图1,平行四边形
的平行四边形,如图1,平行四边形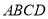 中,
中,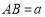 ,
,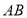 边上的高为
边上的高为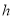 ,我们把
,我们把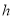 与
与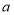 的比值叫做这个平行四边形的“形变比”.
的比值叫做这个平行四边形的“形变比”.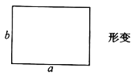
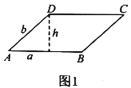
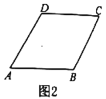
(1)若形变后是菱形
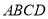 (如图2),则形变前是什么图形?
(如图2),则形变前是什么图形?(2)若图2中菱形
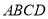 的“形变比”为
的“形变比”为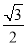 ,求菱形
,求菱形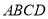 形变前后的面积之比;
形变前后的面积之比;(3)当边长为3,4的矩形变后成为一个内角是30°的平行四边形时,求这个平行四边形的“形变比”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
-
科目: 来源: 题型:
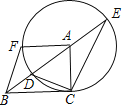
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
-
科目: 来源: 题型:
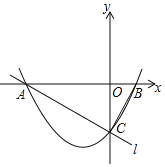
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=
 x2+
x2+ x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,若
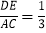 ,则
,则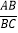 的值为( )
的值为( )
A.
 B.
B. 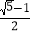 C.
C. 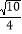 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
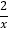 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=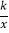 (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.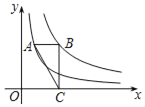
相关试题

