【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
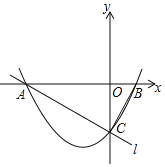
x2+![]() x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() ;(2)DE=
;(2)DE=![]() ;(3)存在点P(
;(3)存在点P(![]() ,
,![]() ),使∠BAP=∠BCO﹣∠BAG,理由见解析.
),使∠BAP=∠BCO﹣∠BAG,理由见解析.
【解析】
(1)根据题目中的函数解析式可以求得点A和点C的坐标,从而可以求得直线l的函数解析式;
(2)根据题意作出合适的辅助线,利用三角形相似和勾股定理可以解答本题;
(3)根据题意画出相应的图形,然后根据锐角三角函数可以求得∠OAC=∠OCB,然后根据题目中的条件和图形,利用锐角三角函数和勾股定理即可解答本题.
(1)∵抛物线y=![]() x2+
x2+![]() x-2,
x-2,
∴当y=0时,得x1=1,x2=-4,当x=0时,y=-2,
∵抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
∴点A的坐标为(-4,0),点B(1,0),点C(0,-2),
∵直线l经过A,C两点,设直线l的函数解析式为y=kx+b,
![]() ,得
,得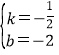 ,
,
即直线l的函数解析式为y=![]() x2;
x2;
(2)直线ED与x轴交于点F,如图1所示,
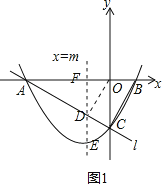
由(1)可得,
AO=4,OC=2,∠AOC=90°,
∴AC=2![]() ,
,
∴OD=![]() ,
,
∵OD⊥AC,OA⊥OC,∠OAD=∠CAO,
∴△AOD∽△ACO,
∴![]() ,
,
即![]() ,得AD=
,得AD=![]() ,
,
∵EF⊥x轴,∠ADC=90°,
∴EF∥OC,
∴△ADF∽△ACO,
∴![]() ,
,
解得,AF=![]() ,DF=
,DF=![]() ,
,
∴OF=4-![]() =
=![]() ,
,
∴m=-![]() ,
,
当m=-![]() 时,y=
时,y=![]() ×(
×(![]() )2+
)2+![]() ×(-
×(-![]() )-2=-
)-2=-![]() ,
,
∴EF=![]() ,
,
∴DE=EF-FD=![]()
![]() =
=![]() ;
;
(3)存在点P,使∠BAP=∠BCO-∠BAG,
理由:作GM⊥AC于点M,作PN⊥x轴于点N,如图2所示,
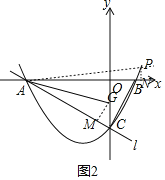
∵点A(-4,0),点B(1,0),点C(0,-2),
∴OA=4,OB=1,OC=2,
∴tan∠OAC=![]() ,tan∠OCB=
,tan∠OCB=![]() ,AC=2
,AC=2![]() ,
,
∴∠OAC=∠OCB,
∵∠BAP=∠BCO-∠BAG,∠GAM=∠OAC-∠BAG,
∴∠BAP=∠GAM,
∵点G(0,-1),AC=2![]() ,OA=4,
,OA=4,
∴OG=1,GC=1,
∴AG=![]() ,
,![]() ,即
,即![]() ,
,
解得,GM=![]() ,
,
∴AM=![]() =
=![]() ,
,
∴tan∠GAM=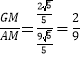 ,
,
∴tan∠PAN=![]() ,
,
设点P的坐标为(n,![]() n2+
n2+![]() n-2),
n-2),
∴AN=4+n,PN=![]() n2+
n2+![]() n-2,
n-2,
∴![]() ,
,
解得,n1=![]() ,n2=-4(舍去),
,n2=-4(舍去),
当n=![]() 时,
时,![]() n2+
n2+![]() n-2=
n-2=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ),
),
即存在点P(![]() ,
,![]() ),使∠BAP=∠BCO-∠BAG.
),使∠BAP=∠BCO-∠BAG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
-
科目: 来源: 题型:
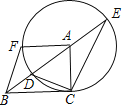
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
-
科目: 来源: 题型:
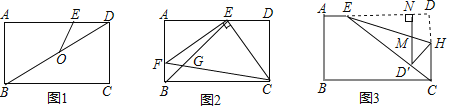
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求
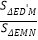 的值;
的值;②连接BE,△D'MH与△CBE是否相似?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,若
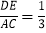 ,则
,则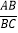 的值为( )
的值为( )
A.
 B.
B. 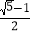 C.
C. 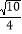 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
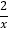 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=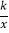 (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.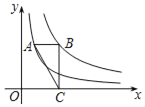
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
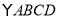 中,
中, 是
是 边上一点,
边上一点,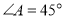 ,
,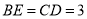 ,
, ,点
,点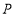 ,
,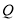 分别是
分别是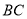 ,
,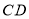 边上的动点,且始终保持
边上的动点,且始终保持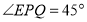 .
.

(1)求
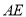 的长;
的长;(2)若四边形
 为平行四边形时,求
为平行四边形时,求 的周长;
的周长;(3)将
 沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段
沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段 的长.
的长.
相关试题

