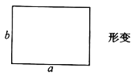
【题目】边长为![]() ,
,![]() 的矩形发生形变后成为边长为
的矩形发生形变后成为边长为![]() ,
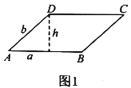
,![]() 的平行四边形,如图1,平行四边形
的平行四边形,如图1,平行四边形![]() 中,
中,![]() ,
,![]() 边上的高为
边上的高为![]() ,我们把
,我们把![]() 与
与![]() 的比值叫做这个平行四边形的“形变比”.
的比值叫做这个平行四边形的“形变比”.
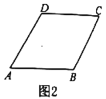
(1)若形变后是菱形![]() (如图2),则形变前是什么图形?
(如图2),则形变前是什么图形?
(2)若图2中菱形![]() 的“形变比”为
的“形变比”为![]() ,求菱形
,求菱形![]() 形变前后的面积之比;
形变前后的面积之比;
(3)当边长为3,4的矩形变后成为一个内角是30°的平行四边形时,求这个平行四边形的“形变比”.
参考答案:
【答案】(1)正方形;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据形变后的图形为菱形,即可推断.
(2)由题意得形变比![]() ,再分别用代数式表示形变前和形变后的面积,计算比值即可.
,再分别用代数式表示形变前和形变后的面积,计算比值即可.
(3)分以AB为底边和以AD为底边两种情况讨论,可求这个平行四边形的“形变比”.
(1)∵形变后是菱形
∴AB=BC=CD=DA
则形变前的四条边也相等
∵四条边相等的矩形是正方形
∴形变前的图形是正方形
(2)根据题意知道:![]()
S形变前=a×b=a2
S形变后=a×h=a×![]() ×a=
×a=![]() a2
a2
∴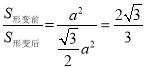
(3)当形变后四边形一个内角为30°时
此时应分两种情况讨论:
第一种:以AB为底边![]() 4×
4×![]() =2
=2
∴这个四边形的形变比为:![]()
第二种:以AD为底边
则![]()
∴这个四边形的形变比为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3
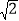 ,AD=2BD,则AF=
,AD=2BD,则AF= .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)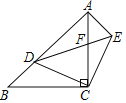
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且∠BDE=15°,DE=4
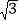 ,DC=2
,DC=2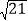 .
.(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
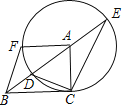
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求
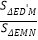 的值;
的值;②连接BE,△D'MH与△CBE是否相似?请说明理由.
相关试题

