【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

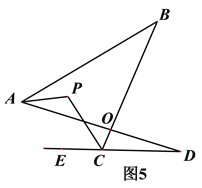
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
参考答案:
【答案】(1)理由见解析;
(2)∠P=26°;
∠P=![]() α+
α+![]() β;
β;![]()
【解析】(1)在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;

(2)如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
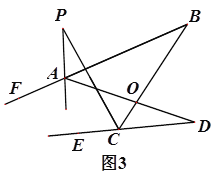
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,
∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°;
×(36°+16°)=26°;
【拓展延伸】
∠P=![]() α+
α+![]() β
β
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示-2的点与表示3的点之间的距离是( )
A. 5 B. -5 C. 1 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x3﹣xy2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,错误的有_____________________
①公理的正确性是用定理证实的;
②证明一个命题是假命题,只要举一反例,即举出一个具备条件,而不具备结论的命题即可;
③要说明一个命题是真命题,只要举出例子,说它的正确性即可;
④假命题不是命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
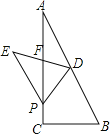
(1)若PD⊥AB,求AP;
(2)若△PDE与△ABC重合部分的面积等于△PAB面积的
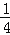 ,求AP的长.
,求AP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式7-2x和5-x的值互为相反数,则x的值为( )
A. 4 B. -4 C. 2 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.a+2b=3ab
B.3a2﹣2a2=1
C.a2a4=a8
D.(﹣a2b)3÷(a3b)2=﹣b
相关试题

