【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
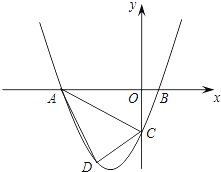
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2+
x2+![]() x﹣3(2)
x﹣3(2)![]() (3)P1(﹣3,﹣3)或P2(
(3)P1(﹣3,﹣3)或P2(![]() ,3)或P3(
,3)或P3(![]() ,3)
,3)
【解析】
(1)把点B(1,0)、C(0,﹣3)标代入抛物线y=ax2+3ax+c求出a,c的值即可;
(2)过点D作DE∥y轴交AC于E,利用待定系数法求出直线AC的解析式,故可得出DE=﹣![]() (m+2)2+3,,再由当m=﹣2时,DE有最大值为3,此时,S△ACD有最大值,从而可求出结论;
(m+2)2+3,,再由当m=﹣2时,DE有最大值为3,此时,S△ACD有最大值,从而可求出结论;
(3) ①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1 ,此时四边形ACP1E1为平行四边形,根据PC两点的纵坐标相等可得出P点坐标;②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,令P(x,3),由![]() x2+
x2+ ![]() x﹣3=3,得出x的值即可得出P点坐标.
x﹣3=3,得出x的值即可得出P点坐标.
(1)解:将点B、C的坐标代入抛物线的解析式得: ![]() ,
,
解得:a= ![]() ,c=﹣3.
,c=﹣3.
∴抛物线的解析式为y= ![]() x2+
x2+ ![]() x﹣3.
x﹣3.
(2)解:令y=0,则 ![]() x2+
x2+ ![]() x﹣3=0,解得x1=1,x2=﹣4,
x﹣3=0,解得x1=1,x2=﹣4,
∴A(﹣4,0)、B(1,0).
令x=0,则y=﹣3,
∴C(0,﹣3),
∴S△ABC= ![]() ×5×3=
×5×3= ![]() .
.
设D(m, ![]() m2+
m2+ ![]() m﹣3),
m﹣3),
过点D作DE∥y轴交AC于E.直线AC的解析式为y=﹣ ![]() x﹣3,则E(m,﹣
x﹣3,则E(m,﹣ ![]() m﹣3),
m﹣3),
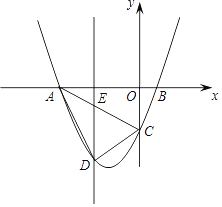
DE=﹣ ![]() m﹣3﹣(
m﹣3﹣( ![]() m2+
m2+ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() (m+2)2+3,
(m+2)2+3,
当m=﹣2时,DE有最大值为3,
此时,S△ACD有最大值为 ![]() ×DE×4=2DE=6.
×DE×4=2DE=6.
∴四边形ABCD的面积的最大值为6+ ![]() =
= ![]() ,
,
(3)解:如图所示:
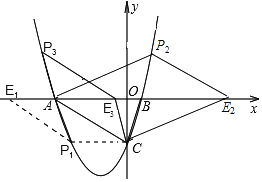
①过点C作CP1∥x轴交抛物线于点P1 , 过点P1作P1E1∥AC交x轴于点E1 , 此时四边形ACP1E1为平行四边形,
∵C(0,﹣3),
∴设P1(x,﹣3),
∴ ![]() x2+
x2+ ![]() x﹣3=﹣3,
x﹣3=﹣3,
解得x1=0,x2=﹣3,
∴P1(﹣3,﹣3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,﹣3),
∴设P(x,3),
∴ ![]() x2+
x2+ ![]() x﹣3=3,
x﹣3=3,
解得x= ![]() 或x=
或x= ![]() ,
,
∴P2( ![]() ,3)或P3(
,3)或P3( ![]() ,3),
,3),
综上所述存在3个点符合题意,坐标分别是P1(﹣3,﹣3)或P2( ![]() ,3)或P3(
,3)或P3( ![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)根据记录的数据可知该厂星期四生产自行车________ 辆;
(2)根据记录的数据可知该厂本周实际生产自行车______辆;
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖励15元;少生产一辆另扣20元,那么该厂工人这一周的工资总额是多少?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
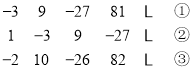
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系;
(3)设
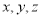 分别为第①②③行的2012个数,求
分别为第①②③行的2012个数,求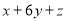 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
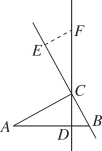
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2与直线y=2x﹣3的图象交于点A(1,b).
(1)求a,b的值;
(2)求两函数图象另一交点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS
 AC,PR
AC,PR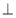 AB,若
AB,若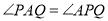 ,PR
,PR PS,则下列结论:①PA平分
PS,则下列结论:①PA平分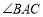 ,②AS
,②AS AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )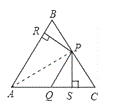
A. 4个B. 3个C. 2个D. 1个
相关试题

