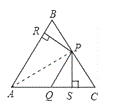
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若
AB,若![]() ,PR
,PR![]() PS,则下列结论:①PA平分
PS,则下列结论:①PA平分![]() ,②AS
,②AS![]() AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
A. 4个B. 3个C. 2个D. 1个
参考答案:
【答案】B
【解析】
根据角平分线判定定理即可推出①,根据勾股定理即可推出②AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出③QP∥AB即可;无法证明△BRP≌△CSP故④错误.
∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,故①正确,
∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2-PR2,AS2=AP2-PS2,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
在△BRP和△CSP中,缺少全等条件,故④错误,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
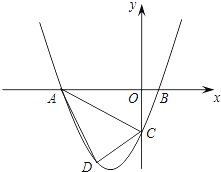
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2与直线y=2x﹣3的图象交于点A(1,b).
(1)求a,b的值;
(2)求两函数图象另一交点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
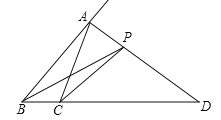
A.a>b B.a=b C.a<b D.不能确定
-
科目: 来源: 题型:
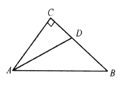
查看答案和解析>>【题目】如图,在
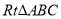 中,
中,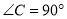 ,
,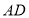 平分
平分 交
交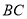 于点
于点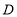 .
.
(1)若BC=7,BD=4,则点
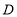 到
到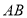 的距离是________;
的距离是________;(2)若
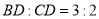 ,点
,点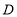 到
到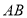 的距离是8,则
的距离是8,则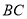 的长是________.
的长是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,sinB=
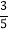 ,
, 
(1)求边BC的长;
(2)将△ABC绕着点C旋转得△A′B′C,点A的对应点A′,点B的对应点B′.如果点A′在BC边上,那么点B和点B′之间的距离等于多少?
相关试题

