【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于点F,连接BD交CE于点G,AE和BD交于点H.
(1)求证:△ACE≌△DCB
(2)求∠BHE的度数

参考答案:
【答案】(1)证明见解析;(2)∠BHE=60°.
【解析】
(1)先由△ACD和△BCE是等边三角形,可知AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,故可得出∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,根据SAS定理即可得△ACE≌△DCB;
(2)利用全等三角形对应角相等得到∠CAE=∠DCB,利用外角性质及等量代换即可求出∠BHE的度数.
(1)∵△ACD,△ECB是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠ECB=60°,
∵∠ACE=∠ACD+∠DCE,∠BCD=∠BCE+∠DCE,∠ACD=∠BCE=60°,
∴∠ACE=∠BCD,
在△ACE和△DCB中,
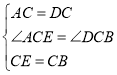 ,
,
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠CAE=∠CDB,
∵∠ACD=∠CDB+∠CBD,∠ACD=60°,
∴∠CAE+∠CBD=60°,
∴∠BHE=∠CAE+∠CBD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有
 、
、 两种商品,已知买一件
两种商品,已知买一件 商品要比买一件
商品要比买一件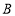 商品少30元,用160元全部购买
商品少30元,用160元全部购买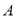 商品的数量与用400元全部购买
商品的数量与用400元全部购买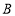 商品的数量相同.
商品的数量相同.(1)求
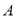 、
、 两种商品每件各是多少元?
两种商品每件各是多少元?(2)如果小亮准备购买
 、
、 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:

①CE=CF;
②线段EF的最小值为
 ;
;③当AD=1时,EF与半圆相切;
④当点D从点A运动到点O时,线段EF扫过的面积是4
 .
.其中正确的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
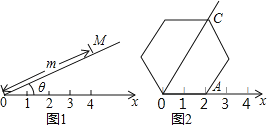
A.(60°,4) B.(45°,4) C.(60°,2
 ) D.(50°,2
) D.(50°,2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
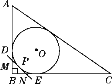
A. r B.
 r C. 2r D.
r C. 2r D.  r
r -
科目: 来源: 题型:
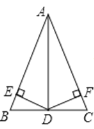
查看答案和解析>>【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=8,FC=6.
(1)求EF的长.
(2)求四边形BEDF的面积.

相关试题

