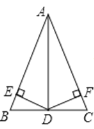
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出BD=DC,∠DEB=∠DFC=90°,根据HL即可证Rt△BDE≌Rt△CDF;(2)由△BDE≌△CDF可得DE=DF,再根据角平分线的判定即可得AD是△ABC的角平分线.
(1)∵点D是BC的中点,
∴BD=DC,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
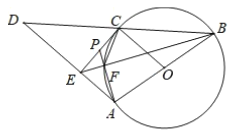
在Rt△BDE和Rt△CDF中
![]() ,
,
∴Rt△BDE≌Rt△CDF(HL);
(2)∵△BDE≌△CDF,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC,
即AD是△ABC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
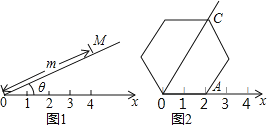
A.(60°,4) B.(45°,4) C.(60°,2
 ) D.(50°,2
) D.(50°,2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于点F,连接BD交CE于点G,AE和BD交于点H.
(1)求证:△ACE≌△DCB
(2)求∠BHE的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
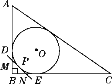
A. r B.
 r C. 2r D.
r C. 2r D.  r
r -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=8,FC=6.
(1)求EF的长.
(2)求四边形BEDF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为圆
为圆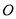 的直径,
的直径,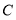 为圆
为圆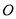 上一点,
上一点,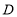 为
为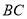 延长线一点,且
延长线一点,且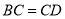 ,
,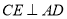 于点
于点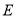 .
.
(1)求证:直线
 为圆
为圆 的切线;
的切线;(2)设
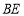 与圆
与圆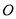 交于点
交于点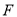 ,
,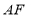 的延长线与
的延长线与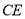 交于点
交于点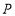 ,
,①求证:

②若
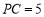 ,
,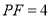 ,求
,求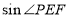 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点
 ,且经过点
,且经过点 ,与
,与 轴分别交于
轴分别交于 两点.
两点.
(1)求直线
 和该抛物线的解析式;
和该抛物线的解析式;(2)如图1,点
 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线 的上方,过点
的上方,过点 作
作 轴的平行线与直线
轴的平行线与直线 交于点
交于点 ,求
,求 的最大值;
的最大值;(3)如图2,
 轴交
轴交 轴于点
轴于点 ,点
,点 是抛物线上
是抛物线上 、
、 之间的一个动点,直线
之间的一个动点,直线 、
、 与
与 分别交于
分别交于 、
、 ,当点
,当点 运动时,求
运动时,求 的值.
的值.
相关试题

