【题目】如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:

①CE=CF;
②线段EF的最小值为![]() ;
;
③当AD=1时,EF与半圆相切;
④当点D从点A运动到点O时,线段EF扫过的面积是4![]() .
.
其中正确的序号是 .
参考答案:
【答案】①③.
【解析】
试题分析:
①连接CD,如图1所示.
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF,
∴CE=CD=CF.故①正确.
②当CD⊥AB时,如图所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=4,∠CBA=30°,
∴∠CAB=60°,AC=2,BC=2![]() .
.
∵CD⊥AB,∠CBA=30°,
∴CD=![]() BC=
BC=![]() .
.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为![]() .
.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为2![]() .故②错误.
.故②错误.
③当AD=1时,连接OC,如图所示.
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=2,AD=1,
∴DO=1.
∴AD=DO,
∴∠ACD=∠OCD=30°,
∵点E与点D关于AC对称,
∴∠ECA=∠DCA,
∴∠ECA=30°,
∴∠ECO=90°,
∴OC⊥EF,
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.故③正确.
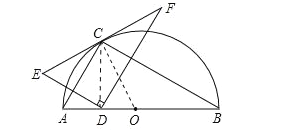
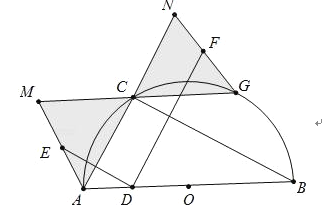
④∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点O时,
点E的运动路径AM与AO关于AC对称,
点F的运动路径NG与AO关于BC对称.
∴EF扫过的图形就是图中阴影部分.
∴S阴影=2S△AOC=2×![]() ACBC=2
ACBC=2![]() .故④错误.
.故④错误.
故答案为①③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. m3×㎡=m5 B. 2m+3n=5mn C. m6÷㎡=m3 D. (m-n)2=㎡-n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.
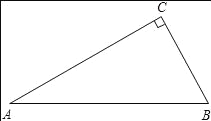
(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.连接BD,求证:BD平分∠CBA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2011内蒙古赤峰,6,3分)在体育课上,初三年级某班10名男生“引体向上”的成绩(单位:次)分别是:9,14,10,15,7,9,16,10,11,9,这组数据的众数、中位数、平均数依次是( )
A. 10,8,11 B. 10,8,9 C. 9,8,11 D. 9,10,11
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.

(1)找出这天载客量的中位数,说明这个中位数的意义;
(2)估计3路公共汽车平均每班的载客量大约是多少?
(3)计算这天载客量在平均载客量以上班次占总班次的百分数.
(注:一个小组的组中值是指这个小组的两个端点数的平均数)
-
科目: 来源: 题型:
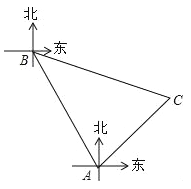
查看答案和解析>>【题目】某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边等于3,一边等于6,则它的周长为( )
A. 12 B. 12或15 C. 15或18 D. 15
相关试题

