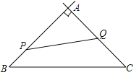
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,现有动点
,现有动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,动点
方向运动,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,已知点
方向运动,已知点![]() 的速度是
的速度是![]() ,点
,点![]() 的速度是
的速度是![]() ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,![]() 的面积是
的面积是![]() 面积的一半?
面积的一半?
参考答案:
【答案】![]() 或
或![]()
【解析】
设经过x秒△APQ的面积是△ABC面积的一半,由点P的速度是4cm/s,点Q的速度是2cm/s表示出BP=4xcm,CQ=2xcm,进而表示出AP=(24-4x)cm,AQ=(16-2x)cm,利用面积列出方程求解即可.
设经过x秒△APQ的面积是△ABC面积的一半,
∵点P的速度是4cm/s,点Q的速度是2cm/s,
∴BP=4xcm,CQ=2xcm,
(1)当AP=(24-4x)cm,AQ=(16-2x)cm,
根据题意得:![]() (24-4x)(16-2x)=
(24-4x)(16-2x)=![]() ×
×![]() ×24×16,
×24×16,
整理得x2-14x+24=0,
解得:x=2或x=12(舍去).
(2)当AP=(4x-24)cm,AQ=(2x-16)cm,
根据题意得:![]() (4x-24)(2x-16)=
(4x-24)(2x-16)=![]() ×
×![]() ×24×16,
×24×16,
整理得x2-14x+24=0,
解得:x=2(舍去)或x=12.
故答案是:2或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
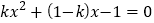 ,下列说法正确的是( )
,下列说法正确的是( )A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
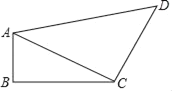
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
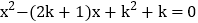 。
。(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
-
科目: 来源: 题型:
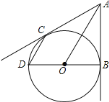
查看答案和解析>>【题目】如图,从
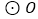 外一点
外一点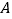 作
作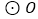 的切线
的切线 ,
,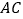 ,切点分别为
,切点分别为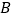 ,
,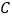 ,
,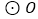 的直径
的直径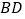 为
为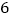 ,连结
,连结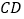 ,
,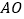 .
.
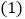 求证:
求证: ;
;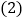 求
求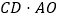 的值;
的值; 若
若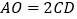 ,求劣弧
,求劣弧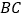 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=80,BC=60, 点D 从点 B 出发,在线段 BA 上以每秒 4 个单位长度的速度向终点A 运动,连结CD. 设点D 运动的时间为 t 秒.
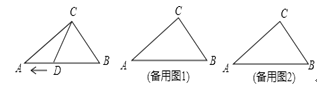
(1)用含 t 的代数式表示 BD 的长.
(2)求AB 的长及 AB 边上的高.
(3)当△BCD 为等腰三角形时,直接写出 t 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
相关试题

