【题目】在图1、图2、图3中,直线MN与线段AB的延长线或AB交于点O,点C和点D在直线MN上,且∠ACM =∠BDM = 45°.

(1)在图1中,点O在AB的延长线上,且AO=3BO,请直接写出AC与BD的数量关系与位置关系;
(2)在图2中,点O在AB上,且AO=BO,写出AC与BD的数量关系与位置关系并证明.
(3)在图3中,点O在AB上,且AO=kBO,求![]() 的值.
的值.
参考答案:
【答案】(1) BD∥AC; AC=3BD;(2) AC⊥BD;AC=BD;(3)k.
【解析】
试题分析:(1)由∠ACM=∠BDM=45°得出BD∥AC,得出△ACO∽△BEO,利用对应边成比例得出答案即可;
(2)过B作BE⊥BD交OD于点E,根据平行线的性质得到∠BED=45°,根据邻补角的定义得到∠OEB=∠ACO=135°,根据全等三角形的性质即可得到结论;
(3)过点B作BE∥CA交DO于E,根据平行线的性质得到∠BEO=∠ACO.根据相似三角形的性质得到![]() .根据已知条件即可得到结论.
.根据已知条件即可得到结论.
试题解析:(1)∵∠ACM=∠BDM=45°,
∴BD∥AC,
∴△ACO∽△BEO,
∴![]() ,
,
又∵AO=3BO,
∴![]() ,
,
即AC=3BD;
(2)过B作BE⊥BD交OD于点E,

∵∠ACM=∠BDM=45°,BE⊥BD,
∴∠BED=∠BDM=45°,
∴BE=BD,∠OEB=∠ACO=135°,
∴AC∥BE,
∵BE⊥BD,
∴AC⊥BD,
在△ACO和△BEO中,
 ,
,
∴△ACO≌△BEO,(AAS)
∴AC=BE,
∴AC=BD;
延长AC交DB的延长线于F,如图2,
∵BE∥AC,
∴∠AFD=90°.
∴AC⊥BD;
(3)如图3,过点B作BE∥CA交DO于E,

∴∠BEO=∠ACO.
又∵∠BOE=∠AOC,
∴△BOE∽△AOC.
∴![]() .
.
又∵AO=kBO,
由(2)的方法易得BE=BD,
∴![]() =k.
=k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若1+2+3+…+n=a , 求代数式(xny)(xn-1y2)(xn-2y3)…(x2yn-1)(xyn)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a-b=2,a-c=1,则(2a-b-c)2+(c-b)2的值为( )
A. 10B. 9C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A , B , C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A , B , C , D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:已知在纸面上有一数轴(如图所示).

操作一:
(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;
操作二:
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数________表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(
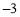 ,0)、(0,4),抛物线
,0)、(0,4),抛物线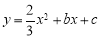 经过B点,且顶点在直线
经过B点,且顶点在直线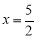 上.
上.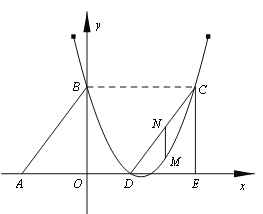
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.
(1)若CF=2,AE=3,求BE的长;
(2)求证:点G为CD中点;
(3)求证:∠AGE=2∠CEG.
相关试题

