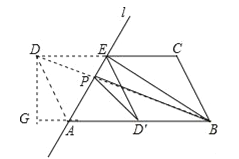
【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;
(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG,DG,根据勾股定理即可得到结论.
试题解析:(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,∴四边形DAD′E是平行四边形,∴DE=AD′,∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC,∴CE=D′B,CE∥D′B,∴四边形BCED′是平行四边形;
∵AD=AD′,∴DAD′E是菱形,(2)∵四边形DAD′E是菱形,∴D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,∵CD∥AB,∴∠DAG=∠CDA=60°,∵AD=1,∴AG=![]() ,DG=
,DG=![]() ,∴BG=
,∴BG=![]() ,∴BD=
,∴BD=![]() =
=![]() ,∴PD′+PB的最小值为
,∴PD′+PB的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A. 从装有10个黑球的不透明袋子中摸出一个球,恰好是红球
B. 抛掷一枚普通正方体骰子所得的点数小于7
C. 抛掷一枚普通硬币,正面朝上
D. 从一副没有大小王的扑克牌中抽出一张牌,恰好是方块
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的表示集合的大括号里.
4,0.5,﹣1 ,10%,﹣5,﹣3.14,0,
,10%,﹣5,﹣3.14,0,  ,+2018
,+2018
(1)正整数集合{…}
(2)分数集合{…}
(3)负有理数集合{…}
(4)整数集合{…}. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题(2)利用乘法分配律及去括号法则先去括号,然后再合并同类项即可;
(1)计算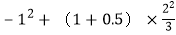
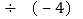
(2)化简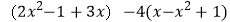
(3)解方程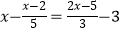
(4)先化简,再求值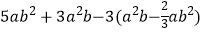 ,其中a=2,b=-1
,其中a=2,b=-1 -
科目: 来源: 题型:
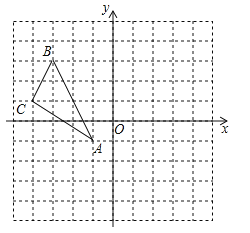
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2,并写出点C的对应点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示:3,﹣3,﹣1
 ,0,4.5,并用“<”按从小到大的顺序连接.
,0,4.5,并用“<”按从小到大的顺序连接. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)(﹣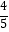 )×13+(﹣
)×13+(﹣ 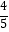 )×2﹣(﹣
)×2﹣(﹣ 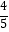 )×5
)×5
(3)﹣22+5×(﹣3)﹣(﹣4)÷4
(4)﹣14﹣(1﹣0.5)× ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
相关试题

