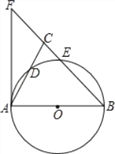
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
参考答案:
【答案】(1)见解析 (2)![]()
【解析】分析:(1)连接BD,由圆周角定理得出∠ADB=90°,由等腰三角形的性质得出∠ABC=2∠ABD,得出∠ABD=∠CAF,证出∠CAF+∠CAB=90°,BA⊥FA,即可得出结论;
(2)连接AE,由圆周角定理得出∠AEB=90°,设CE长为x,则EB长为3x,![]() 由勾股定理可得
由勾股定理可得![]() 在Rt
在Rt![]() 中,由勾股定理得出方程,解方程即可.
中,由勾股定理得出方程,解方程即可.
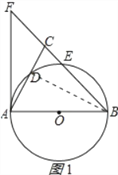
详解:(1)证明:连接BD,如图1所示:
∵AB是⊙O的直径∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD,
∵∠ABC=2∠CAF,∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线;
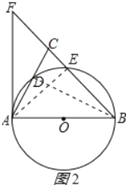
(2)连接AE,如图2所示:
∵AB是⊙O的直径∴∠AEB=90°,即△AEB为直角三角形,
∵![]() 设CE长为x,则EB长为3x,BC长为4x.则AB长为4x,
设CE长为x,则EB长为3x,BC长为4x.则AB长为4x,
在Rt△AEB中由勾股定理可得![]() 在Rt△AEC中,
在Rt△AEC中,![]()
由勾股定理得:![]() ,解得:
,解得:![]()
∵![]()
∴![]()
即CE长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号
甲
乙
每台每小时分拣快递件数(件)
1000
800
每台价格(万元)
5
3
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员
阅读能力
思维能力
表达能力
甲
93
86
73
乙
95
81
79
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
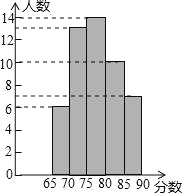
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016吉林省)如图1,在平面直角坐标系中,点B在x轴正半轴上,OB的长度为2m,以OB为边向上作等边三角形AOB,抛物线l:
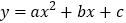 经过点O,A,B三点.
经过点O,A,B三点.(1)当m=2时,a= ,当m=3时,a= ;
(2)根据(1)中的结果,猜想a与m的关系,并证明你的结论;
(3)如图2,在图1的基础上,作x轴的平行线交抛物线l于P、Q两点,PQ的长度为2n,当△APQ为等腰直角三角形时,a和n的关系式为 ;
(4)利用(2)(3)中的结论,求△AOB与△APQ的面积比.
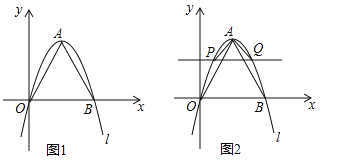
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点
 为直线
为直线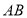 上一点,过点
上一点,过点 作射线
作射线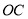 ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(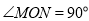 ).
).(1)若
 ,求
,求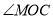 的大小.
的大小.(2)将图①中的三角板绕点
 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边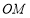 恰好平分
恰好平分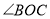 ,问:
,问: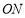 是否平分
是否平分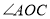 ?请说明理由.
?请说明理由.(3)将图①中的三角板绕点
 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边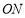 在
在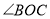 的内部,如果
的内部,如果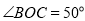 ,则
,则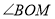 与
与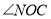 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A.了解我国民众对乐天集团“萨德事件”的看法
B.调查我校某班学生喜欢上数学课的情况
C.了解湖南卫视《人们的名义》反腐剧的收视率
D.调查某类烟花爆竹燃放的安全情况
相关试题

