【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交x轴于B点, ![]()
![]() .
.
![]() 已知点
已知点![]() ,写出点D关于直线AB对称的点
,写出点D关于直线AB对称的点![]() 的坐标;
的坐标;
![]() 现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、
现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、![]() 如图
如图![]() 两点,求证:
两点,求证: ![]() ;
;
![]() 若E是线段OB上一点,
若E是线段OB上一点, ![]() 于G,交AB于F,求
于G,交AB于F,求![]() 的值.
的值.

参考答案:
【答案】(1) ![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】试题分析: ![]() 过D作
过D作![]() 于H,交y轴于
于H,交y轴于![]() ,根据AB为
,根据AB为![]() 的垂直平分线,即可得到
的垂直平分线,即可得到![]() 为D点关于AB的对称点,再根据
为D点关于AB的对称点,再根据![]() ,得到
,得到![]() ,进而得到
,进而得到![]() ,最后得出
,最后得出![]() ;
;
(2)先连接OC,通过判定![]() ≌
≌![]() ,即可得出
,即可得出![]() ;
;
![]() 过B作
过B作![]() 于M,则
于M,则![]() ,通过判定
,通过判定![]() ≌
≌![]() ,得到AG=OM
,得到AG=OM ![]() ,再判定
,再判定![]() ≌
≌![]() ,得到
,得到![]() ,根据AE=AG+GE,OF=OM-FM,即可得到
,根据AE=AG+GE,OF=OM-FM,即可得到![]() ,最后求得
,最后求得![]() 的值
的值![]()
试题解析: ![]() 过D作
过D作![]() 于H,交y轴于
于H,交y轴于![]() ,
,

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为
为![]() 的垂直平分线,
的垂直平分线,
![]() 为D点关于AB的对称点,
为D点关于AB的对称点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 连接OC,
连接OC,

![]() 为AB的中点,
为AB的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
![]() 过B作
过B作![]() 于M,则
于M,则![]() ,
,

![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上依次有
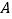 、
、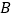 、
、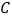 三个港口,甲、乙两船同时分别从
三个港口,甲、乙两船同时分别从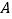 、
、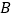 港口出发,沿直线匀速驶向
港口出发,沿直线匀速驶向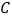 港,最终达到
港,最终达到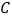 港.设甲、乙两船行驶
港.设甲、乙两船行驶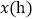 后,与
后,与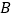 港的距离分别为
港的距离分别为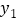 、
、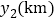 ,
,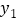 、
、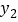 与
与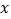 的函数关系如图所示.
的函数关系如图所示. (
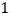 )填空:
)填空: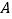 、
、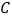 两港口间的距离为__________
两港口间的距离为__________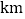 ,
,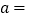 __________.
__________.(
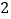 )求图中点
)求图中点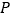 的坐标.
的坐标.(
 )若两船的距离不超过
)若两船的距离不超过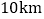 时能够相互望见,求甲、乙两船可以相互望见时
时能够相互望见,求甲、乙两船可以相互望见时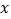 的取值范围.
的取值范围.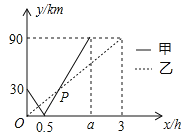
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数轴上5与﹣2所对的两点之间的距离:|5﹣(﹣2)|=7;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣8与﹣5所对的两点之间的距离:|(﹣8)﹣(﹣5)|=3
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|=|b﹣a|
回答下列问题:
(1)数轴上表示﹣2和﹣5的两点之间的距离是_____;
数轴上表示数x和3的两点之间的距离表示为_____;
数轴上表示数_____和_____的两点之间的距离表示为|x+2|,;
(2)七年级研究性学习小组在数学老师指导下,对式子|x+2|+|x﹣3|进行探究:
①请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为:_____.
②请你在草稿纸上画出数轴,要使|x﹣3|+|x+2|=7,数轴上表示点的数x=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案:
方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)例:代数式(a+b)2表示a、b两数和的平方.仿照上例填空:
代数式a2﹣b2表示_____.
代数式(a+b)(a﹣b)表示_____.
(2)试计算a、b取不同数值时,a2﹣b2及(a+b)(a﹣b)的植,填入下表:

(3)请你再任意给a、b各取一个数值,并计算a2﹣b2及(a+b)(a﹣b)的植:
当a=_____,b=_____时,a2﹣b2=_____,(a+b)(a﹣b)=_____.
(4)我的发现:_____.
(5)用你发现的规律计算:78.352﹣21.652.
相关试题

