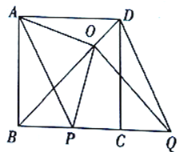
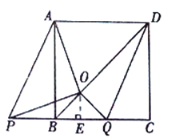
【题目】如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() .边
.边![]() 在其所在的直线上平移,将通过平移得到的线段记为
在其所在的直线上平移,将通过平移得到的线段记为![]() ,连接
,连接![]() 、
、![]() ,并过点
,并过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .
.
(1)请直接写出线段![]() 在平移过程中,四边形
在平移过程中,四边形![]() 是什么四边形;
是什么四边形;
(2)请判断![]() 、
、![]() 之间的数量关系和位置关系,并加以证明;
之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
参考答案:
【答案】(1)四边形![]() 是平行四边形;(2)
是平行四边形;(2)![]() 且
且![]() ,证明见解析;(3)见解析.
,证明见解析;(3)见解析.
【解析】
(1)根据平移的性质,可得PQ=BC=AD,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据正方形的性质,平移的性质,可得PQ与AB的关系,根据等腰直角三角形的判定与性质,可得∠PQO,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式,可得函数关系式.
(1)根据平移的性质可得,PQ=BC,
∵四边形ABCD是正方形,
∴BC=AD,BC∥AD,
∴PQ=AD,PQ∥AD,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)![]() 且
且![]() .证明如下:
.证明如下:
①当![]() 向右平移时,如图,
向右平移时,如图,
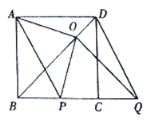
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() ,
,
∴![]() 且
且![]() .
.
②当![]() 向左平移时,如图,
向左平移时,如图,
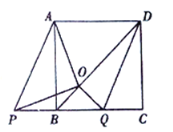
同理可证,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 且
且![]() .
.
(3)过点![]() 作
作![]() 于
于![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
①当![]() 向右平移时,如图,
向右平移时,如图,
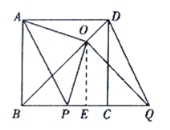
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
②当![]() 向左平移时,如图,
向左平移时,如图,
![]() ,
,
∴![]() .
.
∵![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
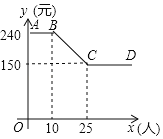
查看答案和解析>>【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
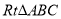 中,
中,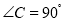 ,
,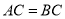 ,直线
,直线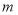 经过点
经过点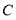 ,分别过点
,分别过点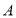 ,
,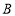 作直线
作直线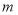 的垂线,垂足分别为点
的垂线,垂足分别为点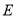 ,
,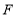 ,若
,若 ,
,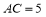 ,则线段
,则线段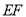 的长为__________.
的长为__________. -
科目: 来源: 题型:
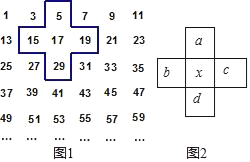
查看答案和解析>>【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
-
科目: 来源: 题型:
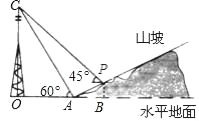
查看答案和解析>>【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
-
科目: 来源: 题型:
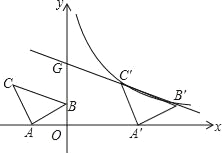
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).
(1)求点C的坐标;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.
(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若点E是
 的中点,求∠F的度数;
的中点,求∠F的度数;(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BEEF的值最大?最大值是多少?

相关试题

