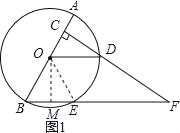
【题目】如图,已知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若点E是![]() 的中点,求∠F的度数;
的中点,求∠F的度数;
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BEEF的值最大?最大值是多少?

参考答案:
【答案】(1)∠F=30°;(2)见解析;(3)当x=![]() 时,最大值=9.
时,最大值=9.
【解析】分析:
(1)如图,连接OE,由OD∥OE可得∠DOE=∠OEB,由点E是![]() 的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
(2)过点O作OM⊥BE于点M,由此可得BE=2BM,再证△OBM≌△DOC可得BM=OC,这样即可得到结论BE=2OC;
(3)由OD∥BF可得△COD∽△CBF,由此可得![]() ,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=
,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=![]() ,从而可得EF=BF-BE=
,从而可得EF=BF-BE=![]() ,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
详解:
(1)如图1,连接OE.
∵![]() ,
,
∴∠BOE=∠EOD,
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)如图1,过O作OM⊥BE于M,
∵OB=OE,
∴BE=2BM,
∵OD∥BF,
∴∠COD=∠B,
在△OBM与△DOC中 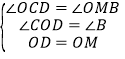 ,
,
∴△OBM≌△DOC,
∴BM=OC,
∴BE=2OC;
(3)∵OD∥BF,
∴△COD∽△CBF,
∴![]() ,
,
∵AC=x,AB=4,
∴OA=OB=OD=2,
∴OC=2﹣x,BE=2OC=4﹣2x,
∴![]() ,
,
∴BF=![]() ,
,
∴EF=BF﹣BE=![]() ,
,
∴BEEF=![]() ,
,
∴当![]() 时,最大值=9.
时,最大值=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
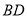 是正方形
是正方形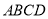 的对角线,
的对角线,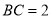 .边
.边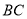 在其所在的直线上平移,将通过平移得到的线段记为
在其所在的直线上平移,将通过平移得到的线段记为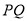 ,连接
,连接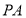 、
、 ,并过点
,并过点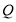 作
作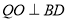 ,垂足为
,垂足为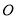 ,连接
,连接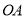 、
、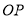 .
.(1)请直接写出线段
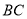 在平移过程中,四边形
在平移过程中,四边形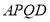 是什么四边形;
是什么四边形;(2)请判断
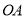 、
、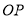 之间的数量关系和位置关系,并加以证明;
之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设
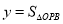 ,
,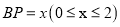 ,求
,求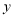 与
与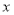 之间的函数关系式.
之间的函数关系式.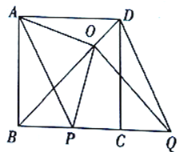
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
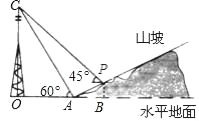
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).
(1)求点C的坐标;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.
(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.
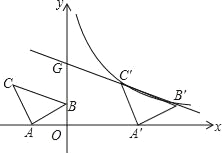
-
科目: 来源: 题型:
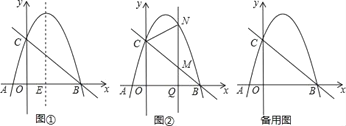
查看答案和解析>>【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨)
1
1.2
1.4
2
2.5
家庭数
4
6
5
3
2
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在20km的环湖越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如右上图所示,根据图中提供的信息,下列说法中错误的有( )
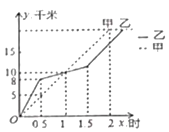
①出发后1小时,两人行程均为10km; ②出发后1.5小时,甲的行程比乙多2km;
③两人相遇前,甲的速度小于乙的速度; ④甲比乙先到达终点.
A. 1个B. 2个C. 3个D. 4个
相关试题

