【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +![]() (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;
(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
参考答案:
【答案】(1)![]() (2)
(2)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)由一次函数图象上点的坐标特征即可得出n1=km1+b、n2=km2+b,二者做差即可得出n1-n2=k(m1-m2),再根据n1-n2+![]() (m1-m2)=0结合m1<m2即可求出k值;(2)由m1+m2=3b、n1+n2=kb+4,即可得出3kb+2b=kb+4,用函数b的代数式表示出k值,根据b的取值范围即可得出k<0,结合一次函数的性质即可得出一次函数y=kx+b中y随x的增大而减小,再根据m1<m2即可得出n1>n2.
(m1-m2)=0结合m1<m2即可求出k值;(2)由m1+m2=3b、n1+n2=kb+4,即可得出3kb+2b=kb+4,用函数b的代数式表示出k值,根据b的取值范围即可得出k<0,结合一次函数的性质即可得出一次函数y=kx+b中y随x的增大而减小,再根据m1<m2即可得出n1>n2.
试题解析:(1)∵点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图象上,
∴n1=km1+b、n2=km2+b,
∴n1n2=(km1+b)(km2+b)=k(m1m2),
∵n1n2+![]() (m1m2)=0,
(m1m2)=0,
∴k(m1m2)+![]() (m1m2)=0,
(m1m2)=0,
∴(k+![]() )(m1m2)=0,
)(m1m2)=0,
∵m1<m2,
∴k=![]() ;
;
(2)n1>n2,理由如下:
∵n1+n2=(km1+b)+(km2+b)=k(m1+m2)+2b=kb+4,,m1+m2=3b,
∴3kb+2b=kb+4,
解得:k=![]() .
.
∵b>2.
∴k=![]() <0,
<0,
∴一次函数y=kx+b中y随x的增大而减小。
又∵m1<m2,
∴n1>n2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1、x2、x3的方差为4,则2 x1+3、2 x2+3、2 x2+3的方差为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数学活动课上,陈老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
(1)理解:
如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;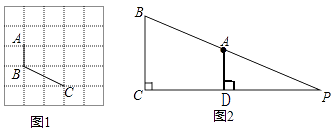
(2)应用:
如图2,在Rt△PBC中,∠PCB=90°,BC=9,点A在BP边上,且AB=13.AD⊥PC,CD=12,若PC上存在符合条件的点M,使四边形ABCM为对等四边形,求出CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于P(m,n),若点Q的坐标为(m,|m-n|),则称点Q为点P的关联点.
(1)请直接写出点(2,2)的关联点;
(2)如果点P在一次函数y=x-1的图像上,其“关联点”Q与点P重合,求点P的坐标;
(3)已知点P在一次函数y=x(x>0)和一次函数y=
 x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数
x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数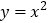 的图像上,求线段PQ的最大值及此时点P的坐标.
的图像上,求线段PQ的最大值及此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直线y=2x-1向上平移动4个单位长度后,所得直线的解析式为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
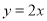 的图象与反比例函数
的图象与反比例函数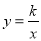 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.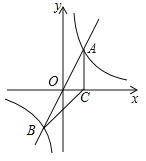
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
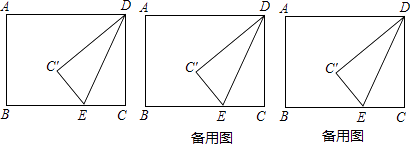
(1)若点C′刚好落在对角线BD上时,BC′=;
(2)当B C′∥DE时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
相关试题

