【题目】如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.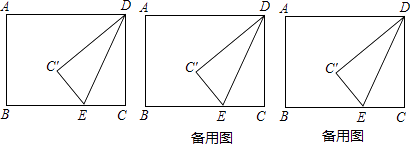
(1)若点C′刚好落在对角线BD上时,BC′=;
(2)当B C′∥DE时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
参考答案:
【答案】
(1)4
(2)
解:如图2,由折叠得,∠CED=∠C′ED,
∵BC′∥DE,
∴∠EC′B=∠C′ED,∠CED=∠C′BE,
∴∠EC′B=∠C′EB,
∴BE=C′E=EC=4;

(3)
解:作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C′在矩形内部时,如图3,

∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
∴由勾股定理得:MC′=2 ![]() ,
,
∴NC′=6﹣2 ![]() ,
,
设EC=x,则C′E=x,NE=4﹣x,
∵NC′2+NE2=C′E2,
∴(6﹣2 ![]() )2+(4﹣x)2=x2,
)2+(4﹣x)2=x2,
解得:x=9﹣3 ![]() ,
,
即CE=9﹣3 ![]() ;
;
②当点C′在矩形外部时,如图4,

∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
∴由勾股定理得:MC′=2 ![]() ,
,
∴NC′=6+2 ![]() ,
,
设EC=y,则C′E=y,NE=y﹣4,
∵NC′2+NE2=C′E2,
∴(6+2 ![]() )2+(y﹣4)2=y2,
)2+(y﹣4)2=y2,
解得:y=9+3 ![]() ,
,
即CE=9+3 ![]() ,
,
综上所述,CE的长为9±3 ![]() .
.
【解析】解:(1)如图1,由折叠可得DC'=DC=6,
∵∠C=90°,BC=8,
∴Rt△BCD中,BD=10,
∴BC′=10﹣6=4.
所以答案是4;
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +
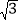 (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直线y=2x-1向上平移动4个单位长度后,所得直线的解析式为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
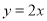 的图象与反比例函数
的图象与反比例函数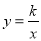 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.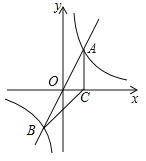
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数y=
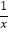 ,下列说法正确的是( )
,下列说法正确的是( )
A.图象经过(1,﹣1)
B.图象位于二、四象限
C.图象是中心对称图形
D.y随x的增大而减小 -
科目: 来源: 题型:
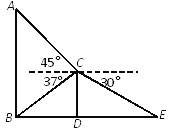
查看答案和解析>>【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:
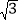 ≈1.73,sin37°≈
≈1.73,sin37°≈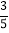 ,tan37°≈
,tan37°≈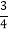 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
相关试题

