【题目】在平面直角坐标系xOy中,对于P(m,n),若点Q的坐标为(m,|m-n|),则称点Q为点P的关联点.
(1)请直接写出点(2,2)的关联点;
(2)如果点P在一次函数y=x-1的图像上,其“关联点”Q与点P重合,求点P的坐标;
(3)已知点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数
x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数![]() 的图像上,求线段PQ的最大值及此时点P的坐标.
的图像上,求线段PQ的最大值及此时点P的坐标.
参考答案:
【答案】(1)(2;0);(2)(2;1) ;(3)PQ的最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)
【解析】试题分析:(1)直接根据关联点的定义可求得答案;(2)设P(x,x-1),由关联点的定义表示出Q点的坐标,由Q与P重合可求得P点的坐标;(3)设点P的坐标为(a,b),由题意可知:a>0,b>0且a>b,2b>a,然后得到点Q的坐标为(a,a-b),再列出PQ与a的函数关系式,最后利用配方法可求得PQ的最大值,以及点P的坐标.
试题解析:(1)点(2,2)的关联点的坐标为(2,|22|),即(2,0).
(2)设P(x,x1),则点P的关联点的坐标为(x,1).
∵点P的“关联点”Q与点P重合,
∴x1=1,解得x=2.
∴点P的坐标为(2,1).
(3)设点P的坐标为(a,b).
∵点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,
x(x>0)所围成的区域内,
∴a>0,b>0且a>b,2b>a.
∴点P的“关联点”Q的坐标为(a,ab).
∵点Q在二次函数y=x2的图象上,
∴ab=a2,整理得b=aa2.
∵PQ=b(ab)=2ba,
∴PQ=2(aa2)a=2a2+a=2(a![]() )2+
)2+![]() .
.
∴当a=![]() 时,PQ有最大值,最大值为
时,PQ有最大值,最大值为![]() .
.
把a=![]() 代入b=aa2得b=
代入b=aa2得b=![]() .
.
∴点P的坐标为(![]() ,
,![]() 6).
6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.

根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】若x1、x2、x3的方差为4,则2 x1+3、2 x2+3、2 x2+3的方差为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数学活动课上,陈老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
(1)理解:
如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;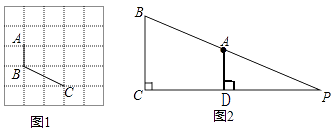
(2)应用:
如图2,在Rt△PBC中,∠PCB=90°,BC=9,点A在BP边上,且AB=13.AD⊥PC,CD=12,若PC上存在符合条件的点M,使四边形ABCM为对等四边形,求出CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +
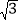 (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直线y=2x-1向上平移动4个单位长度后,所得直线的解析式为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
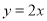 的图象与反比例函数
的图象与反比例函数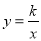 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.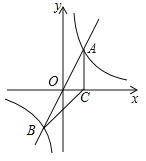
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
相关试题

