【题目】某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6000件,若在国内市场销售,平均每件产品的利润与国内销售量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) |
|
|
若在国外销售,平均每件产品的利润与国外的销售数量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) | 100 |
|
(1)用![]() 的代数式表示
的代数式表示![]() 为:
为:![]() =;
=;
(2)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润为60万元?
参考答案:
【答案】(1)6-x;(2)公司每年国内销售量为2千件,国外的销售量为4千件或国内销售量为6千件,国外的销售量为0件时,可使公司每年的总利润为60万元.
【解析】
(1)由于该公司的年产量为6000件,每年可在国内、国外市场上全部售完,可得国内销售量+国外销售量=6千件,即x+t=6,变形即为t=6-x;
(2)根据平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系y2=![]() 及t=6-x即可求出y2与x的函数关系:当0≤x≤3时,y2=5x+80;当3<x≤6时,y2=100;根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分二种情况讨论:①
及t=6-x即可求出y2与x的函数关系:当0≤x≤3时,y2=5x+80;当3<x≤6时,y2=100;根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分二种情况讨论:①![]() ;②
;②![]() 即可.
即可.
(1)由题意,得x+t=6,
∴t=6-x;
(2)设国内平均每件产品的利润为y1,则有y1=![]()
设平均每件产品的利润为y2则有y2=![]() 且t=6-x,
且t=6-x,
∴y2=![]() ,
,
分两种情况:
①当0≤x≤3时,(15x+90)x+(5x+80)(6-x)=600;
解得,![]() ,
,![]() (舍去)
(舍去)
∴t=6-x=4,
所以,公司每年国内销售量为2千件,国外的销售量为4千件时,可使公司每年的总利润为60万元.
②当3<x≤6时,(-5x+130)x+100(6-x)=600
解得,![]() ,
,![]() (舍去)
(舍去)
∴t=6-x=0,
所以,公司每年国内销售量为6千件,国外的销售量为0件时,可使公司每年的总利润为60万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个长方形放置在平面直角坐标系中,
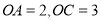 ,点
,点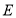 是
是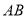 的中点,反比例函数图像过点
的中点,反比例函数图像过点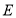 且和
且和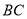 相交于点
相交于点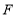 .
.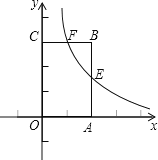
(1)求直线
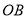 和反比例函数的解析式;
和反比例函数的解析式;(2)求四边形
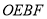 的面积.
的面积. -
科目: 来源: 题型:
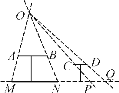
查看答案和解析>>【题目】如图,AB是公园的一圆桌的主视图,MN表示该桌面在路灯下的影子,CD则表示一个圆形的凳子.
(1)请在图中标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径与桌面距地面的距离为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果顺次连接一个四边形各边的中点,得到的新四边形是矩形,则原四边形一定是( )
A.平行四边形B.矩形
C.对角线互相垂直的四边形D.对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程:
(1)(3x+1)2﹣9=0
(2)x2+4x﹣1=0
(3)3x2﹣2=4x
(4)(y+2)2=1+2y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
相关试题

